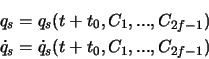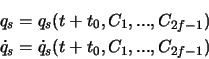Nächste Seite: Erhaltung der Energie
Aufwärts: Vorlesung Physik
Vorherige Seite: Das Zweikörper-Problem
Inhalt
.
Bei der Bewegung eines mechanischen Systems ändern sich die 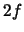 Grössen
Grössen 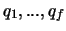 unf
unf
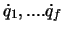 mit der Zeit
mit der Zeit 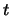 . Es gibt Funktionen
. Es gibt Funktionen 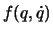 dieser Grössen, die bei der Bewegung ihren Wert erhalten und nur
von den Anfangsbedingungen abhängen. Diese Grössen heissen Erhaltungsgrösse oder Integrale der Bewegung.
Einige davon, die eine erste Integration der BG geliefert haben, haben wir schon getroffen:
dieser Grössen, die bei der Bewegung ihren Wert erhalten und nur
von den Anfangsbedingungen abhängen. Diese Grössen heissen Erhaltungsgrösse oder Integrale der Bewegung.
Einige davon, die eine erste Integration der BG geliefert haben, haben wir schon getroffen: 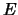 und
und 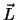 . Wieviele
Integrale der Bewegung gibt es?
Eine einfache Überlegung führt zur Antwort. Man stelle sich vor, dass es uns gelungen ist, die BG vollständig zu
integrieren. Die produzierten
. Wieviele
Integrale der Bewegung gibt es?
Eine einfache Überlegung führt zur Antwort. Man stelle sich vor, dass es uns gelungen ist, die BG vollständig zu
integrieren. Die produzierten 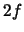 Funktionen lauten
Funktionen lauten
wobei wir eine der Integrationskonstanten in der Form einer zu 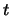 additiven Konstante gewählt haben. Auflösen
dieser Gleichungen nach
additiven Konstante gewählt haben. Auflösen
dieser Gleichungen nach 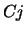 und Elimination der Zeit erlaubt, diese Konstanten - welche nur von den
Anfangsbedingungen abhängen - als Funtkion von
und Elimination der Zeit erlaubt, diese Konstanten - welche nur von den
Anfangsbedingungen abhängen - als Funtkion von 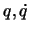 auszudrücken. Bei der Konstruktion sind
diese
auszudrücken. Bei der Konstruktion sind
diese 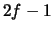 Funtionen die Integrale der Bewegung. Unter diesen Funktionen befinden sich einige,
die eine besondere Bedeutung haben. Das sind solche Erhaltungsgrössen, die aus allgemeinen
Symmetriebetrachtungen hergeleitet werden können. Diese Erhaltungsgrössen können ermittelt
werden, ohne irgendeinen Schritt zur Lösung der BG eingeleitet zu haben: sie hängen eben nur von
der ''Symmetrie'' des Systems ab und treten bei allen Problemen auf, die die gleichen Symmetrien haben.
Durch Symmetrieüberlegungen könnte es uns gelingen, eine teilweise Integration der BG zu
erzielen, ohne dass wir viel Geschick besitzen (Geschick war nämlich im Spiel, als
wir die BW im Kap. 2 ''geschickt'' mit einem Faktor multiplizierten, der dann zur
Energie und Drehimpulserhaltung geführt hat!). Deswegen spielen Symmetrien
eine sehr wichtige Rolle in der modernen Physik. Die Suche nach einer einheitlichen Beschreibung der
Natur beginnt und endet mit der Frage nach der in der Natur zugrunde liegenden Symmetrien (von den Himmelskörpern bis zu den Quarks).
Was meinen wir aber mit dem Satz ''Symmetrie eines Systems''? Und wie führen Symmetrien zur
Existenz von Erhaltungsgrössen? Die Physik gibt auf diese Fragen eine ganz präzise Antwort,
die eigentlich ziemlich universell ist. Es macht deshalb Sinn, die Frage jetzt in der Mechanik zu behandeln.
Funtionen die Integrale der Bewegung. Unter diesen Funktionen befinden sich einige,
die eine besondere Bedeutung haben. Das sind solche Erhaltungsgrössen, die aus allgemeinen
Symmetriebetrachtungen hergeleitet werden können. Diese Erhaltungsgrössen können ermittelt
werden, ohne irgendeinen Schritt zur Lösung der BG eingeleitet zu haben: sie hängen eben nur von
der ''Symmetrie'' des Systems ab und treten bei allen Problemen auf, die die gleichen Symmetrien haben.
Durch Symmetrieüberlegungen könnte es uns gelingen, eine teilweise Integration der BG zu
erzielen, ohne dass wir viel Geschick besitzen (Geschick war nämlich im Spiel, als
wir die BW im Kap. 2 ''geschickt'' mit einem Faktor multiplizierten, der dann zur
Energie und Drehimpulserhaltung geführt hat!). Deswegen spielen Symmetrien
eine sehr wichtige Rolle in der modernen Physik. Die Suche nach einer einheitlichen Beschreibung der
Natur beginnt und endet mit der Frage nach der in der Natur zugrunde liegenden Symmetrien (von den Himmelskörpern bis zu den Quarks).
Was meinen wir aber mit dem Satz ''Symmetrie eines Systems''? Und wie führen Symmetrien zur
Existenz von Erhaltungsgrössen? Die Physik gibt auf diese Fragen eine ganz präzise Antwort,
die eigentlich ziemlich universell ist. Es macht deshalb Sinn, die Frage jetzt in der Mechanik zu behandeln.
Unterabschnitte




Nächste Seite: Erhaltung der Energie
Aufwärts: Vorlesung Physik
Vorherige Seite: Das Zweikörper-Problem
Inhalt
Kraeutler Vincent
2000-05-30