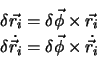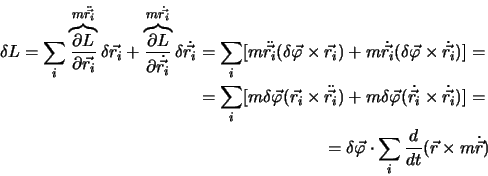Nächste Seite: Skaleninvarianz
Aufwärts: Integrale der Bewegung und
Vorherige Seite: Die Impulserhaltung
Inhalt
Die Drehimpulserhaltung
Eine weitere mögliche Symmetrie eines Systems ist die Rotationsinvarianz.
Man stelle sich vor, alle Ortsvektoren seien instantan um
eine gemeinsame Achse gedreht. Falls 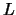 nach der Tansformation so aussieht wie vorher, dann ist
nach der Tansformation so aussieht wie vorher, dann ist 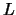 rotationsinvariant.
Zum Beipiel, eine nur vom Abstand abhängige potentielle Energie führt zur Rotationsinvarianz von
rotationsinvariant.
Zum Beipiel, eine nur vom Abstand abhängige potentielle Energie führt zur Rotationsinvarianz von 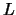 .
Um die Rotationsinvarianz mathematisch zu formulieren, führen wir den Vektor
.
Um die Rotationsinvarianz mathematisch zu formulieren, führen wir den Vektor
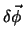 einer infinitesimalen Drehung ein,
deren Betrag gleich dem Drehwinkel
einer infinitesimalen Drehung ein,
deren Betrag gleich dem Drehwinkel 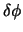 ist und deren Richtung mit der Drehachse zusammenfällt. Danach untersuchen wir,
wie sich als Konsequenz dieser Drehung der Ortsvektor
ist und deren Richtung mit der Drehachse zusammenfällt. Danach untersuchen wir,
wie sich als Konsequenz dieser Drehung der Ortsvektor 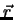 ändert.
ändert.
Durch diese Drehung ändert sich der Abstand 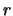 nicht. Die lineare Verschiebung des Endes des Ortsvektors ist mit
dem Winkel
nicht. Die lineare Verschiebung des Endes des Ortsvektors ist mit
dem Winkel 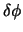 durch die Gleichung
durch die Gleichung
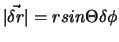 dargestellt, siehe Figur. Der Vektor
dargestellt, siehe Figur. Der Vektor
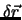 steht
senkrecht auf der durch
steht
senkrecht auf der durch 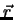 und
und
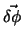 aufgespannten Ebene. Folglich ist
aufgespannten Ebene. Folglich ist
und
Setzen von 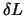 für alle
für alle
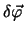 zu Null ergibt die Erhaltungsgrösse
zu Null ergibt die Erhaltungsgrösse
Der Vektor 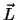 wird Drehimpuls genannt. Die Erhaltung des Drehimpulses haben wir benutzt, um
die Relativbewegung beim Zweikörperproblem auf einer Ebene zu vereinfachen.
Wie beim Impuls, ist auch
wird Drehimpuls genannt. Die Erhaltung des Drehimpulses haben wir benutzt, um
die Relativbewegung beim Zweikörperproblem auf einer Ebene zu vereinfachen.
Wie beim Impuls, ist auch 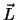 komponentenweise erhalten. In einem Kraftfeld ist aber nur die
Komponente erhalten, die entlang einer Symmetrieachse läuft. Damit eine Symmetrieachse
existiert, muss
komponentenweise erhalten. In einem Kraftfeld ist aber nur die
Komponente erhalten, die entlang einer Symmetrieachse läuft. Damit eine Symmetrieachse
existiert, muss 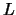 gegenüber der Drehung um diese Achse invariant bleiben.
gegenüber der Drehung um diese Achse invariant bleiben.




Nächste Seite: Skaleninvarianz
Aufwärts: Integrale der Bewegung und
Vorherige Seite: Die Impulserhaltung
Inhalt
Kraeutler Vincent
2000-05-30
![\includegraphics [width=3cm]{f35.eps}](img504.png)
![\includegraphics [width=3cm]{f35.eps}](img504.png)