



Nächste Seite: Die Drehimpulserhaltung
Aufwärts: Integrale der Bewegung und
Vorherige Seite: Erhaltung der Energie
Inhalt
Die Impulserhaltung
Eine weitere mögliche Symmetrie der Lagrange Funktion ist die Translationsinvarianz.
Diese bedeutet folgendes: Man nehme alle Ortsvektoren und füge instantan einen festen
beliebigen Vektor
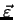 hinzu:
hinzu:
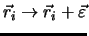 . Sollte,
nach dieser Transformation, die Lagrange Funktion gleich aussehen wie vor der Transformation, dann ist das System
translationsinvariant. Abgeschlossene Systeme mit potentieller Energie, die nur von Differenzvektoren abhängen, sind translationsinvariant.
Mit
. Sollte,
nach dieser Transformation, die Lagrange Funktion gleich aussehen wie vor der Transformation, dann ist das System
translationsinvariant. Abgeschlossene Systeme mit potentieller Energie, die nur von Differenzvektoren abhängen, sind translationsinvariant.
Mit
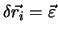 und
und
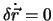 bekommen wir
bekommen wir
Die Translationsinvarianz fordert 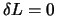 , für jeden
, für jeden 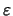 . Das führt zu
. Das führt zu
d.h. die Grösse
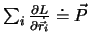 ist ein Integral der Bewegung, und heisst
Gesamtimpuls aller Massenpunkte. Solange
ist ein Integral der Bewegung, und heisst
Gesamtimpuls aller Massenpunkte. Solange 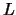 translationsinvariant ist, bleibt das Gesamtimpuls erhalten.
Durch Differenzieren der Lagrange Funktion finden wir,
dass der Impuls sich folgendermassen durch die Geschwindigkeit der Massenpunkte ausdrückt:
translationsinvariant ist, bleibt das Gesamtimpuls erhalten.
Durch Differenzieren der Lagrange Funktion finden wir,
dass der Impuls sich folgendermassen durch die Geschwindigkeit der Massenpunkte ausdrückt:
d.h. der Impuls ist die Summe aller der Impulse der einzelnen Massen.
Die Impulserhaltung haben wir schon in Kap. 2 benutzt, zwar nicht offensichtlich aber entscheidend
für eine Vereinfachung des Zweikörperproblems.
Die Konstanz von 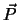 kann man in der Tat benutzen, um einen fiktiven Ortsvektor
kann man in der Tat benutzen, um einen fiktiven Ortsvektor 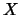 zu definieren,
der trotz der Komplikation
eines Mehrkörperproblems, eine geradlinige Bewegung durchführt, mit konstanter Geschwindigkeit: In der Tat,
zu definieren,
der trotz der Komplikation
eines Mehrkörperproblems, eine geradlinige Bewegung durchführt, mit konstanter Geschwindigkeit: In der Tat,
mit der Masse 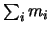 hat den Impuls
hat den Impuls 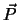 .
.
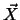 bezeichnet den Ort des Schwerpunktes des Massensystems. Die
Impulserhaltung führt deswegen zur gleichmässigen Bewegung des Schwerpunktes und suggeriert
eine geeignete Linearkombination von Ortsvektoren, die
beim Zweikörperproblem zu einer enormen Vereinfachung des Problems geführt hat.
Die Bedingung
bezeichnet den Ort des Schwerpunktes des Massensystems. Die
Impulserhaltung führt deswegen zur gleichmässigen Bewegung des Schwerpunktes und suggeriert
eine geeignete Linearkombination von Ortsvektoren, die
beim Zweikörperproblem zu einer enormen Vereinfachung des Problems geführt hat.
Die Bedingung
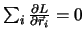 ist zur Aussage
ist zur Aussage
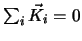 äquivalent,
d.h. die Summe aller Kräfte
ist null. Die Impulserhaltung gilt koordinatenweise, d.h. die drei
Komponenten des Gesamptimpulses sind getrennt erhalten. Sollte in einer gegebenen Richtung ein
homogenes externes Kraftfeld
äquivalent,
d.h. die Summe aller Kräfte
ist null. Die Impulserhaltung gilt koordinatenweise, d.h. die drei
Komponenten des Gesamptimpulses sind getrennt erhalten. Sollte in einer gegebenen Richtung ein
homogenes externes Kraftfeld 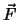 herrschen, dann sind nur solche Komponenten erhalten, die
zum Kraftfeld senkrecht sind.
herrschen, dann sind nur solche Komponenten erhalten, die
zum Kraftfeld senkrecht sind.  bewegt sich mit der BG
bewegt sich mit der BG
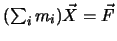 .
Die Impulserhaltung hat, wie die Energieerhaltung, eine weitere Anwendung in der Physik: sie dient
dem Zweck, Aussagen über gewisse Vorgänge zu machen, ohne eigentlich die BG lösen zu
müssen - wenn nur die Lage zu bestimmten Zeiten gesucht ist. Zu diesem Punkt merke man, dass der Gesamtimpuls
immer die Summe aller Impulse ist, unabhängeig von der Existenz oder der Art der Wechselwirkung.
Ein besonders illustratives Beipiel der
Impulserhaltung ist die Herleitung der Raketengleichung.
Eine Rakete enthält einen Vorrat von Atomen, von denen jedes die Masse
.
Die Impulserhaltung hat, wie die Energieerhaltung, eine weitere Anwendung in der Physik: sie dient
dem Zweck, Aussagen über gewisse Vorgänge zu machen, ohne eigentlich die BG lösen zu
müssen - wenn nur die Lage zu bestimmten Zeiten gesucht ist. Zu diesem Punkt merke man, dass der Gesamtimpuls
immer die Summe aller Impulse ist, unabhängeig von der Existenz oder der Art der Wechselwirkung.
Ein besonders illustratives Beipiel der
Impulserhaltung ist die Herleitung der Raketengleichung.
Eine Rakete enthält einen Vorrat von Atomen, von denen jedes die Masse 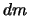 besitze, und eine
Maschine, die die Atome relativ zur Rakete beschleunigt und mit der Geschwindigkeit
besitze, und eine
Maschine, die die Atome relativ zur Rakete beschleunigt und mit der Geschwindigkeit 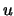 relativ zur Rakete hinten ausstösst.
relativ zur Rakete hinten ausstösst.
Abbildung 3.2:
Schema einer Rakete
|
|
Beim Start sei die Rakete in Ruhestellung. Die Startmasse der Rakete sei  .
Wir betrachten eine horizontal zur Erde gerichtete Rakete. Da keine äusseren Kräfte wirken,
bleibt der Gesamtimpuls des Systems ``Rakete + ausgestossene Atome'' konstant.
Diese Kostante ist 0, da die Rakete beim Start in Ruhe ist. Unser Bezugssystem befindet sich
dort, wo die Rakete zur Zeit
.
Wir betrachten eine horizontal zur Erde gerichtete Rakete. Da keine äusseren Kräfte wirken,
bleibt der Gesamtimpuls des Systems ``Rakete + ausgestossene Atome'' konstant.
Diese Kostante ist 0, da die Rakete beim Start in Ruhe ist. Unser Bezugssystem befindet sich
dort, wo die Rakete zur Zeit  in Ruhe ist (und wo der Schwerpunkt bleibt).
in Ruhe ist (und wo der Schwerpunkt bleibt).
- Schritt:
Abbildung 3.3:
1. Schritt
|
|
Abbildung 3.4:
2. Schritt
|
|
Wir benutzen die Konstanz des Gesamtimpulses :
Aufgelöst:
- Schritt
Aufgelöst:
- n-ter Schritt
Der Geschwindigkeitszuwachs von Schritt zu Schritt beträgt
Die Anzahl 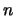 der ausgestossenen Atome ist so gross, dass man
der ausgestossenen Atome ist so gross, dass man 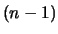 durch
durch 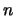 ersetzen kann,
ohne viel falsch zu machen.
ersetzen kann,
ohne viel falsch zu machen.
Wir berücksichtigen jetzt, dass in einer Zeit 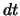 ein Atom ausgestossen wird,
sodass - zur Zeit
ein Atom ausgestossen wird,
sodass - zur Zeit 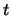 -
- 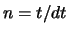 Atome ausgestossen werden. Die ausgestossene Masse ist
Atome ausgestossen werden. Die ausgestossene Masse ist
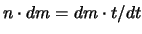 .
. 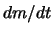 ist eine Eigenschaft der Maschine, die in der Rakete steckt:
Nennen wir sie
ist eine Eigenschaft der Maschine, die in der Rakete steckt:
Nennen wir sie 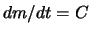 . Obige Gleichung wird dann zu
. Obige Gleichung wird dann zu
Die Summe des Geschwindigkeitszuwachses 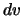 vom Start
vom Start 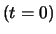 bis zur Zeit
bis zur Zeit 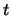 ,
ergibt die Geschwindigkeit der Rakete zur Zeit
,
ergibt die Geschwindigkeit der Rakete zur Zeit 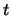 :
:
Nun ist 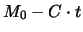 gerade die Masse der Rakete zur Zeit
gerade die Masse der Rakete zur Zeit 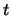 , so dass man schreiben kann
, so dass man schreiben kann
Typische Werte für die Ausstossgeschwindigkeit liegen bei 4000 m/sec für ein
Wasserstoff-Sauerstoff-Brennstoffgemisch bei einer Gastemperatur von 4000 C,
sodass eine Rakete beträchtliche Geschwindigkeiten erreichen kann, wenn z.B. der
Brennstoffvorrat etwa die Hälfte der Gesamtmasse der Rakete beträgt.
C,
sodass eine Rakete beträchtliche Geschwindigkeiten erreichen kann, wenn z.B. der
Brennstoffvorrat etwa die Hälfte der Gesamtmasse der Rakete beträgt.
Die Beschleunigung der Rakete ist
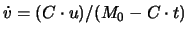 .
Die Beschleunigung kann der Schubkraft des Raketenantriebes zugeschrieben werden.
Die Schubkraft ist
.
Die Beschleunigung kann der Schubkraft des Raketenantriebes zugeschrieben werden.
Die Schubkraft ist
Die Schubkraft ist das Produkt der Geschwindigkeit, mit der die Atome ausgestossen werden,
mal der Anzahl der Atome, die pro Zeiteinheit ausgestossen werden.
Dieses Beispiel zeigt, dass wieder einmal ein Erhaltungssatz zum Aufbau einer DG benutzt wurde.




Nächste Seite: Die Drehimpulserhaltung
Aufwärts: Integrale der Bewegung und
Vorherige Seite: Erhaltung der Energie
Inhalt
Kraeutler Vincent
2000-05-30
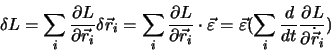
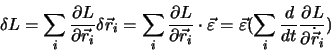
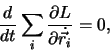
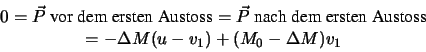
![]() ein Atom ausgestossen wird,
sodass - zur Zeit
ein Atom ausgestossen wird,
sodass - zur Zeit ![]() -
- ![]() Atome ausgestossen werden. Die ausgestossene Masse ist
Atome ausgestossen werden. Die ausgestossene Masse ist
![]() .
. ![]() ist eine Eigenschaft der Maschine, die in der Rakete steckt:
Nennen wir sie
ist eine Eigenschaft der Maschine, die in der Rakete steckt:
Nennen wir sie ![]() . Obige Gleichung wird dann zu
. Obige Gleichung wird dann zu

![]() .
Die Beschleunigung kann der Schubkraft des Raketenantriebes zugeschrieben werden.
Die Schubkraft ist
.
Die Beschleunigung kann der Schubkraft des Raketenantriebes zugeschrieben werden.
Die Schubkraft ist