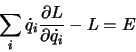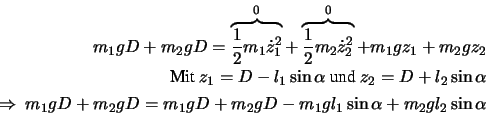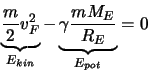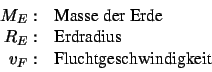Nächste Seite: Die Impulserhaltung
Aufwärts: Integrale der Bewegung und
Vorherige Seite: Integrale der Bewegung und
Inhalt
Erhaltung der Energie
Wir beginnen mit dem Erhaltungssatz, der aus der Homogenität der Zeit folgt. Wir untersuchen
das Verhalten von 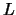 unter der Zeitverschiebung
unter der Zeitverschiebung
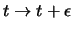 für ein abgeschlossenes System, wobei
für ein abgeschlossenes System, wobei 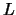 nicht explizit von der Zeit
abhängt. Dieses Verhalten ist so zu verstehen: Die potentielle Energie
enthält den Abstand zwischen den Massen, der sich mit der Zeit verändert. Eine Zeittranslation
bewegt die Massen entlang der Bahn und führt deswegen zu einer Änderung des Ortsvektors
nicht explizit von der Zeit
abhängt. Dieses Verhalten ist so zu verstehen: Die potentielle Energie
enthält den Abstand zwischen den Massen, der sich mit der Zeit verändert. Eine Zeittranslation
bewegt die Massen entlang der Bahn und führt deswegen zu einer Änderung des Ortsvektors
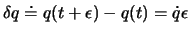 und der potentiellen Energie. Das Gleiche
erfährt die kinetischen Energie, wobei
und der potentiellen Energie. Das Gleiche
erfährt die kinetischen Energie, wobei
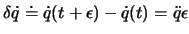 ist.
Sollten sich beispielsweise auch die Massen mit der Zeit ändern, (etwa durch Streuung in den Weltraum),
dann würde
ist.
Sollten sich beispielsweise auch die Massen mit der Zeit ändern, (etwa durch Streuung in den Weltraum),
dann würde 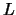 einen zusätzlichen Term bekommen, der aber in einem abgeschlossenen System
verboten ist. Die Variation
einen zusätzlichen Term bekommen, der aber in einem abgeschlossenen System
verboten ist. Die Variation
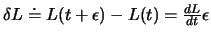 berechnet sich wie folgt:
berechnet sich wie folgt:
Wenn wir fordern, dass 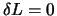 , dann folgt die Gleichung
, dann folgt die Gleichung
Hieraus folgt die Erhaltungsgrösse
die bei der Bewegung eines abgeschlossenen Systems erhalten bleibt. Diese Grösse heisst die
Energie eines Systems. In kartesischen Koordinaten
ist
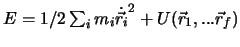 , d.h. die Summe der kinetischen und
der potentiellen Energie.
Integrale der Bewegung führen nicht nur zur teilweisen Integration der BG, sondern man kann daraus auch
Schlüsse über die Zustände des Systems zu ausgewählten Zeiten der Bahn ziehen, ohne die
Bahn genau zu kennen.
, d.h. die Summe der kinetischen und
der potentiellen Energie.
Integrale der Bewegung führen nicht nur zur teilweisen Integration der BG, sondern man kann daraus auch
Schlüsse über die Zustände des Systems zu ausgewählten Zeiten der Bahn ziehen, ohne die
Bahn genau zu kennen.
Beispiel: Hebelarmgesetz.
Man betrachte einen Hebel wie in der Figur.
Abbildung 3.1:
Zur Herleitung des Hebelarmgesetzes
|
|
Zur Zeit  seien beide Massen auf der gleichen Höhe
seien beide Massen auf der gleichen Höhe 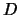 in Ruhe. Lässt man sie los, werden sie ihre
Gleichgewichtslage nur erreichen, wenn
in Ruhe. Lässt man sie los, werden sie ihre
Gleichgewichtslage nur erreichen, wenn 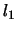 und
und 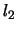 geeignet
gewählt werden. Um
geeignet
gewählt werden. Um 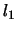 und
und 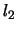 zu bestimmen, schreiben wir den Energiesatz.
zu bestimmen, schreiben wir den Energiesatz.
Die Gleichgewichtsbedingung ist
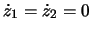 . Eingesetzt in den Energiesatz ergibt
dies die bekannte Hebelarmgleichung.
. Eingesetzt in den Energiesatz ergibt
dies die bekannte Hebelarmgleichung.
Beispiel: Fluchtgeschwindigkeit von der Erde.
Eine Masse 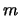 soll von der Erde unendlich weit weg transportiert werden.
Mit welcher Geschwindigkeit soll man sie von der Erdoberfläche wegschiessen?
soll von der Erde unendlich weit weg transportiert werden.
Mit welcher Geschwindigkeit soll man sie von der Erdoberfläche wegschiessen?
Um aus dem Schwerfeld der Erde entweichen zu können, bedarf es mindestens einer
Geschwindigkeit von  beim Erreichen von
beim Erreichen von  .
Die Erhaltung der Energie ergibt die Gleichung
.
Die Erhaltung der Energie ergibt die Gleichung
Damit ist
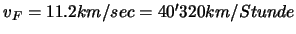 .
.




Nächste Seite: Die Impulserhaltung
Aufwärts: Integrale der Bewegung und
Vorherige Seite: Integrale der Bewegung und
Inhalt
Kraeutler Vincent
2000-05-30
![\begin{eqnarray*}
\frac{dL}{dt}\epsilon & = & \sum_{i}[ \frac{\partial L}{\parti...
...rtial \dot q_i} + \frac{\partial L}{\partial \dot q_i}\ddot q_i]
\end{eqnarray*}](img438.png)
![\begin{eqnarray*}
\frac{dL}{dt}\epsilon & = & \sum_{i}[ \frac{\partial L}{\parti...
...rtial \dot q_i} + \frac{\partial L}{\partial \dot q_i}\ddot q_i]
\end{eqnarray*}](img438.png)
![\begin{displaymath}
\frac{d}{dt}[\sum_i\dot q_i\frac{\partial L}{\partial \dot q_i} - L] = 0
\end{displaymath}](img440.png)