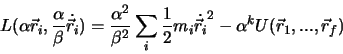Nächste Seite: Schwingungen
Aufwärts: Integrale der Bewegung und
Vorherige Seite: Die Drehimpulserhaltung
Inhalt
Eine weitere mögliche Symmetrie eines mechanischen Systems ist die Skaleninvarianz.
Diese Symmetrie erlaubt, wichtige Schlüsse über die Eigenschaften der Bewegung zu ziehen,
ohne explizit die BG zu lösen. Skaleninvarianz spielt in vielen Gebieten der Physik eine wichtige
Rolle. Beispielsweise in der Nähe eines Phasenübergangs, besitzt ein makroskopisches System
die Skaleninvarianz, und diese Tatsache legt sein Verhalten ziemich eindeutig fest, ohne dass
viel über die Einzelheiten der für den Phasenübergang verantworlichen Wechselwirkung bekannt sein muss.
Wir wollen am Beispiel der Mechanik diese wichtige Symmetrie beschreiben.
Wir untersuchen den Fall, wo die potentielle Energie eine homogene Funktion der Koordinaten ist:
Hierin ist 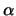 eine beliebige Konstante und
eine beliebige Konstante und 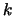 der Grad der Homogenität der Funktion.
Wir führen nun eine Transformation durch, bei welcher alle Koordinaten mit der Konstante
der Grad der Homogenität der Funktion.
Wir führen nun eine Transformation durch, bei welcher alle Koordinaten mit der Konstante 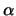 multipliziert werden, und die Zeit mit der Konstante
multipliziert werden, und die Zeit mit der Konstante 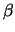 :
:
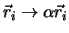 ,
,
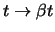 . Durch diese Transformation wird
. Durch diese Transformation wird 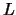 zu
zu
Wenn man 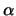 und
und 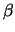 durch die Bedingung
durch die Bedingung
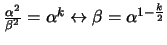 verknüpft, bekommt die Lagrange Funktion den selben Vorfaktor
verknüpft, bekommt die Lagrange Funktion den selben Vorfaktor 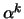 , d.h. die BG bleiben unverändert.
Multiplikation aller Koordinaten mit dem selben Faktor führt zu neuen Bahnen, die den
Ursprünglichen ähnlich sind und sich lediglich in den linearen Abmessungen von ihnen
unterscheiden. Auf diesen geometrisch ähnlichen Bahnen verhalten sich alle Zeitdifferenzen
zwischen entsprechenden Bahnpunkten wie
, d.h. die BG bleiben unverändert.
Multiplikation aller Koordinaten mit dem selben Faktor führt zu neuen Bahnen, die den
Ursprünglichen ähnlich sind und sich lediglich in den linearen Abmessungen von ihnen
unterscheiden. Auf diesen geometrisch ähnlichen Bahnen verhalten sich alle Zeitdifferenzen
zwischen entsprechenden Bahnpunkten wie
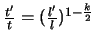 , wobei
, wobei 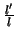 das Verhältnis der linearen
Abmessung zweier Bahnen darstellt.
Beispiel 1. Nehmen wir unser vertrautes Galilei Experiment. Multipliziert man die
Koordinate
das Verhältnis der linearen
Abmessung zweier Bahnen darstellt.
Beispiel 1. Nehmen wir unser vertrautes Galilei Experiment. Multipliziert man die
Koordinate 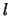 mit einer Zahl, so wird die Masse tiefer gebracht, sagen wir zum Punkt
mit einer Zahl, so wird die Masse tiefer gebracht, sagen wir zum Punkt  .
Damit die gleichen BG gelten, muss sich die Zeit zu
.
Damit die gleichen BG gelten, muss sich die Zeit zu
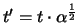 (
( im homogenen
Feld der Erde) transformiert haben. Das ergibt
im homogenen
Feld der Erde) transformiert haben. Das ergibt
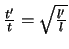 . Das ist das Fallgesetz von
Galileo, hergeleitet allein aus Symmetrieüberlegungen, ohne einmal die BG formuliert zu haben.
Beispeil 2. Für die potentielle Energie zwischen zwei Massen gilt
. Das ist das Fallgesetz von
Galileo, hergeleitet allein aus Symmetrieüberlegungen, ohne einmal die BG formuliert zu haben.
Beispeil 2. Für die potentielle Energie zwischen zwei Massen gilt 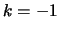 . Die Multiplikation der Koordinate
mit einer Zahl bewirkt den Übergang auf eine ähnliche Ellipse. Die Gleichung
. Die Multiplikation der Koordinate
mit einer Zahl bewirkt den Übergang auf eine ähnliche Ellipse. Die Gleichung
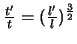 besagt, dass die Quadrate der Umlaufzeiten mit der dritten Potenz der Dimension der Ellipse variieren. Das ist ein
eleganter Beweis des 3. Keplerschen Gesetzes.
Beispeil 3. Für eine eindimensionale Bewegung mit
besagt, dass die Quadrate der Umlaufzeiten mit der dritten Potenz der Dimension der Ellipse variieren. Das ist ein
eleganter Beweis des 3. Keplerschen Gesetzes.
Beispeil 3. Für eine eindimensionale Bewegung mit  (harmonische Oszillator) bedeutet die Gleichung
(harmonische Oszillator) bedeutet die Gleichung
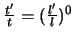 , dass die Zeiten
für eine vollständige Schwingung nicht von deren Amplitude abhängen.
, dass die Zeiten
für eine vollständige Schwingung nicht von deren Amplitude abhängen.




Nächste Seite: Schwingungen
Aufwärts: Integrale der Bewegung und
Vorherige Seite: Die Drehimpulserhaltung
Inhalt
Kraeutler Vincent
2000-05-30