



Nächste Seite: Einige wichtige Kräfte der
Aufwärts: Die Bewegungsgleichungen
Vorherige Seite: Einführung
Inhalt
Das Hamilton-Prinzip
Leider benötigt die Formulierung der Bewegungsgleichungen - wie alle Gesetze der Physik -
einen gewissen Grad an Abstraktion. Diese Abstraktion ist, neben der Beobachtung,
eine weitere Eigenschaft, die die Physik kennzeichnet.
Abstraktion bedeutet oft die Einführung von Hilfsgrössen,
die keinen unmittelbaren experimentellen Zugang haben und deshalb eher
mathematischer Natur sind.
Seit den Arbeiten von R.P. Feynman (wie Newton und Einstein
einer der Grossen der Physik) wissen wir, dass eine allgemeine Methode,
physikalische Gesetze zu formulieren, im Prinzip der kleinsten Wirkung
( principle of least action) liegt.
Dieses Prinzip wurde von W.R. Hamilton in der Mechanik 1823 eingeführt, und erlaubt, die Bewegungsgleichungen aufzustellen.
Die für seine Formulierung benötigten abtsrakten Grössen wollen wir anhand des Experimentsvon Galileo einführen. Gegeben
sei ein Massenpunkt 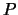 , der sich auf einer Höhe
, der sich auf einer Höhe 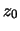 zur Zeit
zur Zeit 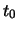 befindet.
Lässt man
befindet.
Lässt man 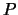 fallen, so verringert sich seine Höhe, während seine Geschwindigkeit
gleichzeitig zunimmt. Zur Zeit
fallen, so verringert sich seine Höhe, während seine Geschwindigkeit
gleichzeitig zunimmt. Zur Zeit 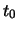 besitzt
besitzt 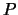 aus sich heraus (dadurch dass er auf einer bestimmten Höhe ist)
die Fähigkeit, Geschwindigkeit zu gewinnen.
Diese Fähigkeit drücken die Physiker mit
dem Begriff der potentiellen Energie aus. Die potenzielle Energie ist eine skalare Grösse, d.h.
sie kann nur eine Funktion von
aus sich heraus (dadurch dass er auf einer bestimmten Höhe ist)
die Fähigkeit, Geschwindigkeit zu gewinnen.
Diese Fähigkeit drücken die Physiker mit
dem Begriff der potentiellen Energie aus. Die potenzielle Energie ist eine skalare Grösse, d.h.
sie kann nur eine Funktion von
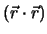 sein. Die einfachste Wahl für
sein. Die einfachste Wahl für 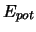 im Galileo Experiment ist
im Galileo Experiment ist
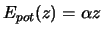 , wobei wir
, wobei wir 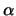 später bestimmen. Mit dieser Wahl drücken wir
die Tatsache aus, dass je höher
später bestimmen. Mit dieser Wahl drücken wir
die Tatsache aus, dass je höher 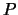 liegt, die Geschwindigkeit dementsprechend zunehmen kann,
bevor er auf die Erde trifft. Wir könnten auch weitere Potenzen von
liegt, die Geschwindigkeit dementsprechend zunehmen kann,
bevor er auf die Erde trifft. Wir könnten auch weitere Potenzen von 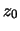 berücksichtigen (das wäre sogar richtiger,
wie wir später zeigen werden). Wir wollen aber sehen, ob dieser einfache lineare Ansatz genügt,
um den Fallvorgang zu beschreiben. Die einfachste skalare Grösse, die man mit einem Vektor
berücksichtigen (das wäre sogar richtiger,
wie wir später zeigen werden). Wir wollen aber sehen, ob dieser einfache lineare Ansatz genügt,
um den Fallvorgang zu beschreiben. Die einfachste skalare Grösse, die man mit einem Vektor 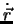 bilden kann, ist
bilden kann, ist
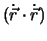 , sodass die Energie, die mit der Geschwindigkeit assoziert ist,
, sodass die Energie, die mit der Geschwindigkeit assoziert ist,
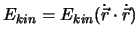 sein muss.
Wir werden später sehen, dass die einfachste Wahl, die sich anbietet -
sein muss.
Wir werden später sehen, dass die einfachste Wahl, die sich anbietet -
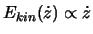 - falsch ist: die niedrigste
Potenz, die mit den Experimenten in Einklang ist,
ist
- falsch ist: die niedrigste
Potenz, die mit den Experimenten in Einklang ist,
ist
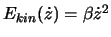 , wobei wir seit Einstein wissen, dass auch diese Wahl nur eine Näherung für
, wobei wir seit Einstein wissen, dass auch diese Wahl nur eine Näherung für 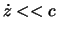 , mit
(
, mit
(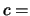 Lichtgeschwindigkeit
Lichtgeschwindigkeit 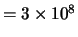 m/sec) ist. Durch die Einführung der abtstrakten Begriffe
m/sec) ist. Durch die Einführung der abtstrakten Begriffe
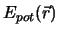 und
und
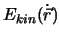 sind wir imstande, das Hamilton Prinzip zu formulieren. Dem Massenpunkt
sind wir imstande, das Hamilton Prinzip zu formulieren. Dem Massenpunkt 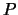 ordnen wir die Lagrange
Funktion zu:
ordnen wir die Lagrange
Funktion zu:
![\begin{displaymath}
L[ \vec{r}(t), \dot {\vec{r}} (t)] =E_{kin}(\dot{ \vec r}) - E_{pot}(\vec r)
\end{displaymath}](img182.png)
die im Fall vom Galileo Experiment zu
 wird.
Der Begriff des Feldes stellt ein fundamentales Konzept in der Physik dar. Man unterscheidet zwischen
Skalarfeldern und Vektorfeldern. Ein Skalarfeld
wird.
Der Begriff des Feldes stellt ein fundamentales Konzept in der Physik dar. Man unterscheidet zwischen
Skalarfeldern und Vektorfeldern. Ein Skalarfeld
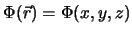 ist eine skalarwertige Funktion
dreier unabhängiger Variablen, wobei sich die Zahl drei auf die Dimension unseres Raumes bezieht.
ist eine skalarwertige Funktion
dreier unabhängiger Variablen, wobei sich die Zahl drei auf die Dimension unseres Raumes bezieht.
Beispiel: Wir betrachten die Funktion
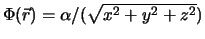 . Graphisch stellt man solche
Felder durch 2-dimensionale Schnitte dar, in denen die Flächen
. Graphisch stellt man solche
Felder durch 2-dimensionale Schnitte dar, in denen die Flächen
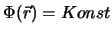 (Äquipotentialfläche)
als Höhenlinien erscheinen. Der Abstand der Linien enstpricht dabei gleichen Wertunterschieden der Konstanten.
(Äquipotentialfläche)
als Höhenlinien erscheinen. Der Abstand der Linien enstpricht dabei gleichen Wertunterschieden der Konstanten.
Beispiel: Die Lagrange Funktion des Galileo Experiments kann man als zweidimensionales Skalarfeld 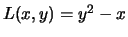 darstellen.
darstellen.
Ein Vektorfeld ordnet jedem Punkt im Raum eine vektorwertige Funktion
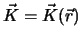 zu.
zu.
Beispiel: Das Gravitationsfeld eines Masssenpunktes ist gegeben durch
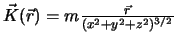 .
.
Graphisch lassen sich Vektorfelder durch 2-dimensionale Schnitte darstellen, in denen die Flächen konstanter
Feldstärke
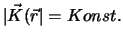 als Höhenlinien erscheinen, an denen man das Feld lokal durch
einen Vektorpfeil charakterisiert. Vektorfelder kann man auch mittels Feldlinien darstellen, wobei das Feld tangential
zur Feldlinie verläuft. Die Dichte der Feldlinien ist dann ein Mass für die Stärke des Feldes.
als Höhenlinien erscheinen, an denen man das Feld lokal durch
einen Vektorpfeil charakterisiert. Vektorfelder kann man auch mittels Feldlinien darstellen, wobei das Feld tangential
zur Feldlinie verläuft. Die Dichte der Feldlinien ist dann ein Mass für die Stärke des Feldes.
Abbildung 1.9:
Graphische Darstellung eines Skalarfeldes
|
|
Abbildung 1.10:
Graphische Darstellung von 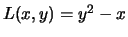
|
|
Abbildung 1.11:
Graphische Darstellung eines Vektorfeldes
|
|
Abbildung 1.12:
Konstruktion zur Berechnung von  (links) und graphische Deutung des Gradienten (rechts)
(links) und graphische Deutung des Gradienten (rechts)
|
|
Für Skalarfelder kann man den Begriff der partiellen Ableitung einführen:
(und ähnlich für 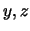 ). Damit lässt sich die räumliche Änderung der Skalarfelder beschreiben.
Wir betrachten
zwei Punkte
). Damit lässt sich die räumliche Änderung der Skalarfelder beschreiben.
Wir betrachten
zwei Punkte  und
und 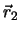 , die durch eine kleine Strecke
, die durch eine kleine Strecke 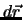 voneinander getrennt sind.
voneinander getrennt sind.
Die Änderung
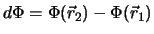 ist gegeben durch die folgende Summe:
ist gegeben durch die folgende Summe:
wobei
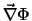 der Gradient von
der Gradient von 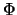 und
und  das totale Differential des Feldes
das totale Differential des Feldes 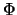 sind. Der
Gradient lässt sich deuten, indem man
sind. Der
Gradient lässt sich deuten, indem man 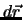 in die Richtung wählt, so dass
in die Richtung wählt, so dass 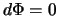 in dieser Richtung ist. Aus der
Gleichung
in dieser Richtung ist. Aus der
Gleichung
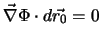 folgt, dass
folgt, dass
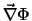 senkrecht auf
senkrecht auf 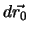 steht. Anderseits definiert
steht. Anderseits definiert 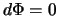 Flächen
Flächen  , so dass
, so dass
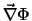 senkrecht auf den Äquipotentialflächen steht. Sein Betrag ist ein Mass für die Stärke der Änderung von
senkrecht auf den Äquipotentialflächen steht. Sein Betrag ist ein Mass für die Stärke der Änderung von 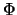 ,
wenn man senkrecht zu den Äquipotentialflächen fortschreitet.
,
wenn man senkrecht zu den Äquipotentialflächen fortschreitet.
Für ein Vektorfeld kann man den Begriff des Linienintegrals einführen (in der Physik spricht man von ''Arbeit'' 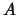 oder
oder 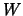 ).
Die Arbeit, die wir aufbringen müssen, um einen Gegenstand von Punkt
).
Die Arbeit, die wir aufbringen müssen, um einen Gegenstand von Punkt 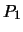 zu
Punkt
zu
Punkt 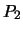 entlang des Wegs
entlang des Wegs 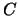 zu bewegen, ist definiert als Wegintegral der Kraft
zu bewegen, ist definiert als Wegintegral der Kraft
mit
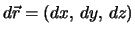 . Das Inkrement
. Das Inkrement 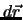 ist ein Vektor,
die Arbeit hingegen ist aufgrund des Skalarproduktes ein Skalar.
ist ein Vektor,
die Arbeit hingegen ist aufgrund des Skalarproduktes ein Skalar.
Abbildung 1.13:
Zur Definition der Arbeit einer Kraft
|
|
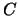 ist hierbei die Bezeichnung für die Raumkurve
ist hierbei die Bezeichnung für die Raumkurve  zwischen dem
Anfangspunkt
zwischen dem
Anfangspunkt
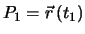 und dem Endpunkt
und dem Endpunkt
 .
Wir geben nun eine Möglichkeit an, das Linienintegral explizit zu berechnen.
Dazu zerlegen wir das Vektorfeld
.
Wir geben nun eine Möglichkeit an, das Linienintegral explizit zu berechnen.
Dazu zerlegen wir das Vektorfeld 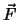 in seine kartesischen Komponenten und
setzen dies in das Integral ein:
in seine kartesischen Komponenten und
setzen dies in das Integral ein:
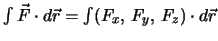 .
Die kartesischen Komponenten
.
Die kartesischen Komponenten 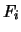 sind noch eine Funktion des Ortes, d.h.
sind noch eine Funktion des Ortes, d.h.
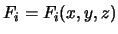 mit
mit 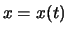 ,
, 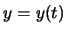 und
und 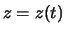 .
Für das Integral benötigen wir die Komponenten des Vektorfeldes
.
Für das Integral benötigen wir die Komponenten des Vektorfeldes 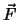 entlang
der Raumkurve in Abhängigkeit des Parameters
entlang
der Raumkurve in Abhängigkeit des Parameters 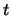 . Wir erhalten dies, indem wir
die entsprechenden Komponenten der Raumkurve
. Wir erhalten dies, indem wir
die entsprechenden Komponenten der Raumkurve  in
in 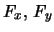 und
und 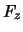 einsetzen. Für
einsetzen. Für 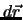 schreiben wir
schreiben wir
 .
Für das Arbeitsintegral ergibt sich durch Einsetzen
.
Für das Arbeitsintegral ergibt sich durch Einsetzen
Damit übersetzen wir das Linienintegral in die Summe gewöhnlicher eindimensionaler Integrale.
Beispiel. Das Vektorfeld 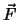 und die Raumkurve
und die Raumkurve  seien gegeben durch
seien gegeben durch
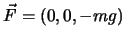 und
und
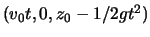 . Die von der Kraft geleistete Arbeit zwischen den Zeiten
. Die von der Kraft geleistete Arbeit zwischen den Zeiten 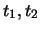 ist
ist
Falls
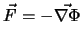 , heisst das Vektorfeld konservativ. Für solche Felder, welche Kraftfelder sind, gilt
, heisst das Vektorfeld konservativ. Für solche Felder, welche Kraftfelder sind, gilt
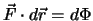 Somit ist
Somit ist
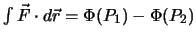 :
Wegintegrale über konservative Felder zwischen den Punkten
:
Wegintegrale über konservative Felder zwischen den Punkten 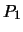 und
und 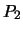 sind unabhängig vom
explizit gewählten Weg, und sind nur vom Wert des skalaren Feldes am Anfangspunkt
sind unabhängig vom
explizit gewählten Weg, und sind nur vom Wert des skalaren Feldes am Anfangspunkt 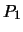 und am Endpunkt
und am Endpunkt
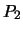 abhängig.
abhängig.
Nach dem Hamilton Prinzip verläuft die Bewegung eines mechanischen Systems von einem gegebenen Anfangspunkt zur
Zeit 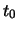 zu einem gegebenenm Endpunkt zur Zeit
zu einem gegebenenm Endpunkt zur Zeit 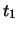 derart, dass die Wirkung
derart, dass die Wirkung
minimal ist (Prinzip der kleinsten Wirkung).
![$S[\vec{r}, \dot {\vec {r}}]$](img243.png) ist ein Funktional,
das allen möglichen Bahnen
ist ein Funktional,
das allen möglichen Bahnen
![$[\vec{r}(t),\dot{\vec{r}}(t)]$](img244.png) eine reelle Zahl zuordnet - den Wert des Integrals. Eine Möglichkeit,
dieses Prinzip zu benutzen, um die physikalische Bahn zu finden, ist die Auswahl vieler Bahnen, unter welchen
eine reelle Zahl zuordnet - den Wert des Integrals. Eine Möglichkeit,
dieses Prinzip zu benutzen, um die physikalische Bahn zu finden, ist die Auswahl vieler Bahnen, unter welchen 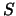 minimalisiert
wird. In diesem Sinne ist das Hamilton Prinzip ein Variationsprinzip, d.h. man versucht durch variieren der Bahn jene zu finden,
die
minimalisiert
wird. In diesem Sinne ist das Hamilton Prinzip ein Variationsprinzip, d.h. man versucht durch variieren der Bahn jene zu finden,
die 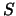 minimiert. Es ist heutzutage nicht ungewöhnlich, dass viele Probleme der Naturwissenschaft (inklusive der Biologie) als
Variationsprinzip formuliert werden. Damit wird das Problem der Suche nach dem Minimum eines geeigneten Funktionals reduziert -
ein ideales Terrain für die heutigen Supercomputer. Oft wird die Suche nach der Lösung folgendermassen gestaltet: man erzeugt
eine Schar von Funktionen, die aus irgendeinem Grund ''physikalisch'' sein könnten. Diese Funktionen werden geeignet parametrisiert
und es werden solche Parameter gesucht, die
minimiert. Es ist heutzutage nicht ungewöhnlich, dass viele Probleme der Naturwissenschaft (inklusive der Biologie) als
Variationsprinzip formuliert werden. Damit wird das Problem der Suche nach dem Minimum eines geeigneten Funktionals reduziert -
ein ideales Terrain für die heutigen Supercomputer. Oft wird die Suche nach der Lösung folgendermassen gestaltet: man erzeugt
eine Schar von Funktionen, die aus irgendeinem Grund ''physikalisch'' sein könnten. Diese Funktionen werden geeignet parametrisiert
und es werden solche Parameter gesucht, die 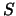 minimalisieren. Die so ermittelte Funktion ist dann eine Möglichkeit für die korrekte Lösung,
wobei ein Funktional oft viele Minima besitzt, so dass die Suche nach dem absoluten Minimum weitere Optimierungsschritte erfordert.
minimalisieren. Die so ermittelte Funktion ist dann eine Möglichkeit für die korrekte Lösung,
wobei ein Funktional oft viele Minima besitzt, so dass die Suche nach dem absoluten Minimum weitere Optimierungsschritte erfordert.
Wir wollen diesen möglichen Lösungsweg am Galileo-Experiment illustrieren. Wir beginnen
mit der Vermutung (um ein Variationsproblem vernünftig zu lösen, muss man eine ''Vermutung'' über die mögliche Bahn
haben), dass
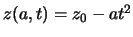 ist.
ist. 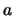 ist hier der sogenannte Variationsparameter, der so gewählt werden muss,
damit
ist hier der sogenannte Variationsparameter, der so gewählt werden muss,
damit 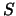 minimal wird. Damit ist
minimal wird. Damit ist
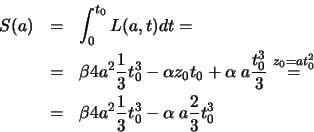
Die Bahn wird variiert, aber die Randpunkte sollen fest sein. Wir setzen 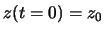 und
und 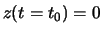 ein. Die Wirkung
berechnet über die möglichen Bahnen
ein. Die Wirkung
berechnet über die möglichen Bahnen
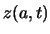 zwischen diesen festen Randpunkten ist
zwischen diesen festen Randpunkten ist
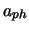 bestimmen wir als Lösung der Gleichung
bestimmen wir als Lösung der Gleichung
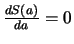 , d.h.
, d.h.
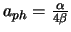 .
Der Vergleich dieses theoretischen Resultats mit dem experimentellen Resultat
.
Der Vergleich dieses theoretischen Resultats mit dem experimentellen Resultat
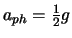 erlaubt, das
Verhältnis des bis jetzt unbekannten Parameters
erlaubt, das
Verhältnis des bis jetzt unbekannten Parameters 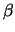 und
und 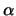 zu bestimmen:
zu bestimmen:
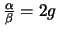 . Mit Hilfe dieses Prinzips haben wir eine eindeutige Voraussage erlangt, die mit dem
Experimemt verifiziert werden kann: legen wir
. Mit Hilfe dieses Prinzips haben wir eine eindeutige Voraussage erlangt, die mit dem
Experimemt verifiziert werden kann: legen wir 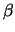 fest, dann ist auch
fest, dann ist auch 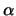 festgelegt. Mit der Wahl
festgelegt. Mit der Wahl
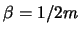 , müssen wir
, müssen wir 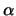 zu
zu 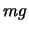 umwandeln, damit das Hamilton Prinzip mit dem Experiment
konsistent ist. Damit kennen wir auch die genaue Form der Lagrange Funktion für das Galileo Experiment.
umwandeln, damit das Hamilton Prinzip mit dem Experiment
konsistent ist. Damit kennen wir auch die genaue Form der Lagrange Funktion für das Galileo Experiment.
Wir hätten anders argumentieren können. Angenommen die Koeffizienten 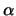 und
und
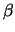 seien bekannt, dann besagt unser Variationsprinzip, dass
seien bekannt, dann besagt unser Variationsprinzip, dass 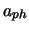 von
von 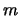 unabhängig ist.
Wir haben damit eine Voraussage produziert, die man experimentell testen kann.
Ist der Test erfolgreich, so freuen wir uns, dass aus einem so abstrakten Prinzip direkt eine
solch konkrete (und gewissermassen überraschende) experimentelle Tatsache folgt.
unabhängig ist.
Wir haben damit eine Voraussage produziert, die man experimentell testen kann.
Ist der Test erfolgreich, so freuen wir uns, dass aus einem so abstrakten Prinzip direkt eine
solch konkrete (und gewissermassen überraschende) experimentelle Tatsache folgt.
Ein zweiter möglicher Weg zur Lösung des Variationsprinzips von Hamilton führt zu den Bewegungsgleichungen.
Zum Studium diseses zweiten Wegs wollen wir zunächst Variationsprobleme im Allgemeinen diskutieren.
Gegeben sei die integrierbare Funktion
Wir suchen eine Funktion 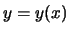 , so daß das Funktional
, so daß das Funktional
einen Extremalwert annimmt. Angenommen,
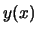 sei eben diese Funktion, die
sei eben diese Funktion, die  Ęzu einem Minimum macht. Dann wächst
Ęzu einem Minimum macht. Dann wächst  wenn
wenn 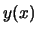 durch eine Funktion der Form
durch eine Funktion der Form
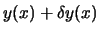 ersetzt ist.
ersetzt ist. 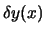 ist eine beliebige differenzierbare Funktion, die
an den Endpunkten verschwindet.
ist eine beliebige differenzierbare Funktion, die
an den Endpunkten verschwindet.
und heisst Variation der Funktion 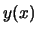 .
.
Abbildung 1.14:
Die Variation von 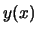
|
|
Die Änderung von  beim Einsetzen von
beim Einsetzen von
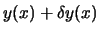 ist die Variation des Funktionals
ist die Variation des Funktionals ![$I [y(x)]$](img268.png) :
:
Die Entwicklung dieser Differenz nach Potenzen von 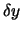 und
und 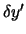 im Integranden beginnt mit Gliedern erster
Ordnung. Die notwendige Bedingung, dass
im Integranden beginnt mit Gliedern erster
Ordnung. Die notwendige Bedingung, dass  extremal ist, ist das Verschwinden dieser Glieder. Nach Ausführung der
Taylor Entwicklung erhalten wir
extremal ist, ist das Verschwinden dieser Glieder. Nach Ausführung der
Taylor Entwicklung erhalten wir
Wenn man berücksichtigt, dass
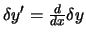 ist, dann lässt sich der zweite Integrand partiell integrieren:
ist, dann lässt sich der zweite Integrand partiell integrieren:
Da die Endpunkte fest sein sollen,
verschwindet der ausintegrierte Term, und die Extremalbedingung
lautet
Da 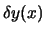 eine beliebige Funktion sein kann, ist diese Gleichung
allgemein nur dann erfüllt, wenn
eine beliebige Funktion sein kann, ist diese Gleichung
allgemein nur dann erfüllt, wenn
ist.
Diese Beziehung heißt Euler-Lagrange-Gleichung. Sie
stellt eine notwendige Bedingung für einen Extremwert des Integrals
 dar.
dar.
Wir kehren zurück zum Hamilton Prinzip. Hierbei wird die Zeit als
Koordinate nicht variiert. Das System durchläuft einen Bahnpunkt und
den dazugehörigen variierten Bahnpunkt zur gleichen Zeit. Es gilt also  .
Ausgehend vom Integral
.
Ausgehend vom Integral
führen wir die
Variation durch. Die Variation einer Bahnkurve 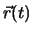 beschreiben wir durch
beschreiben wir durch
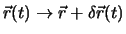 , wobei
, wobei
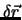 an den Endpunkten verschwinden soll:
an den Endpunkten verschwinden soll:
 . Da die Zeit nicht variiert wird, folgt
. Da die Zeit nicht variiert wird, folgt
wobei 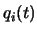 die
die 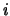 -te Koordinate darstellt. Wegen
-te Koordinate darstellt. Wegen
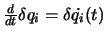 , liefert die
partielle Integration des zweiten Summanden
, liefert die
partielle Integration des zweiten Summanden
Da 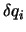 an den Endpunkten (Integralgrenzen) verschwindet,
erhalten wir für die Variation des Integrals
an den Endpunkten (Integralgrenzen) verschwindet,
erhalten wir für die Variation des Integrals
Das Integral verschwindet nur dann, wenn der Koeffizient eines jeden
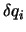 verschwindet. Daraus folgen die Lagrange-Gleichungen der Mechanik:
verschwindet. Daraus folgen die Lagrange-Gleichungen der Mechanik:
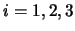 . Das sind die Bewegungsgleichungen. Sie sind eine
Folge des Variationsprinzips, so wie alle Gleichungen der Physik eine Folge eines Variationsprinzips
sind (oder sein sollten).
Für einen Massenpunkt
. Das sind die Bewegungsgleichungen. Sie sind eine
Folge des Variationsprinzips, so wie alle Gleichungen der Physik eine Folge eines Variationsprinzips
sind (oder sein sollten).
Für einen Massenpunkt 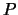 mit der Lagrange Funktion
mit der Lagrange Funktion
![$ L[ \vec{r}(t), \dot {\vec{r}} (t)] = 1/2 m \dot{ \vec r}^2 - U(\vec r)$](img291.png) , bekommen wir
, bekommen wir
Diese wurden, in dieser Form, von Newton gefunden. Deswegen heissen die Lagrange Gleichungen eines
Massenpunktes in kartesischen Koordinaten auch Newton Gleichungen. Wichtige Fragen der Physik wurden
durch die explizite Lösung dieser Gleichungen beantwortet.
Die BG sind Differentialgleichungen (DG). Sie lassen sich eindeutig lösen,
wenn die Anfangsbedingungen bekannt sind. Die Struktur dieser Differentialgleichungen suggeriert,
dass zwei Angaben als Anfangsbedingungen notwendig und hinreichend sind:
Ort und Geschwindigkeit zu einer bestimmen Zeit.
Die Terme in den Newton Gleichungen haben folgende Bedeutung: Die zweite zeitliche Ableitung von 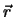 ist die Beschleunigung von
ist die Beschleunigung von 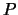 , und beschreibt
die Änderung der Geschwindigkeit. Die negative Ableitung der potentiellen Energie ist die
Kraft, die für die Änderung der Geschwindigkeit verantwortlich ist.
Die Beschleunigung wird in den Einheiten
, und beschreibt
die Änderung der Geschwindigkeit. Die negative Ableitung der potentiellen Energie ist die
Kraft, die für die Änderung der Geschwindigkeit verantwortlich ist.
Die Beschleunigung wird in den Einheiten 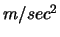 gemessen, die Kraft misst man in
gemessen, die Kraft misst man in
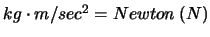 . Die Energie ist deshalb
. Die Energie ist deshalb
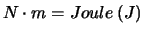 .
Am Beispiel von Galileo nehmen die BG eine besonders einfache Form an.
Die potentielle Energie, die der Ursprung der Kraft ist, ist bekannterweise
.
Am Beispiel von Galileo nehmen die BG eine besonders einfache Form an.
Die potentielle Energie, die der Ursprung der Kraft ist, ist bekannterweise 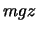 .
Die Kraft ist
.
Die Kraft ist
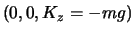 . Die Bewegungsgleichungen lauten
. Die Bewegungsgleichungen lauten
und deren Lösung, mit
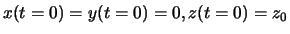 :
:




Nächste Seite: Einige wichtige Kräfte der
Aufwärts: Die Bewegungsgleichungen
Vorherige Seite: Einführung
Inhalt
Kraeutler Vincent
2000-05-30
![]() , der sich auf einer Höhe
, der sich auf einer Höhe ![]() zur Zeit
zur Zeit ![]() befindet.
Lässt man
befindet.
Lässt man ![]() fallen, so verringert sich seine Höhe, während seine Geschwindigkeit
gleichzeitig zunimmt. Zur Zeit
fallen, so verringert sich seine Höhe, während seine Geschwindigkeit
gleichzeitig zunimmt. Zur Zeit ![]() besitzt
besitzt ![]() aus sich heraus (dadurch dass er auf einer bestimmten Höhe ist)
die Fähigkeit, Geschwindigkeit zu gewinnen.
Diese Fähigkeit drücken die Physiker mit
dem Begriff der potentiellen Energie aus. Die potenzielle Energie ist eine skalare Grösse, d.h.
sie kann nur eine Funktion von
aus sich heraus (dadurch dass er auf einer bestimmten Höhe ist)
die Fähigkeit, Geschwindigkeit zu gewinnen.
Diese Fähigkeit drücken die Physiker mit
dem Begriff der potentiellen Energie aus. Die potenzielle Energie ist eine skalare Grösse, d.h.
sie kann nur eine Funktion von
![]() sein. Die einfachste Wahl für
sein. Die einfachste Wahl für ![]() im Galileo Experiment ist
im Galileo Experiment ist
![]() , wobei wir
, wobei wir ![]() später bestimmen. Mit dieser Wahl drücken wir
die Tatsache aus, dass je höher
später bestimmen. Mit dieser Wahl drücken wir
die Tatsache aus, dass je höher ![]() liegt, die Geschwindigkeit dementsprechend zunehmen kann,
bevor er auf die Erde trifft. Wir könnten auch weitere Potenzen von
liegt, die Geschwindigkeit dementsprechend zunehmen kann,
bevor er auf die Erde trifft. Wir könnten auch weitere Potenzen von ![]() berücksichtigen (das wäre sogar richtiger,
wie wir später zeigen werden). Wir wollen aber sehen, ob dieser einfache lineare Ansatz genügt,
um den Fallvorgang zu beschreiben. Die einfachste skalare Grösse, die man mit einem Vektor
berücksichtigen (das wäre sogar richtiger,
wie wir später zeigen werden). Wir wollen aber sehen, ob dieser einfache lineare Ansatz genügt,
um den Fallvorgang zu beschreiben. Die einfachste skalare Grösse, die man mit einem Vektor ![]() bilden kann, ist
bilden kann, ist
![]() , sodass die Energie, die mit der Geschwindigkeit assoziert ist,
, sodass die Energie, die mit der Geschwindigkeit assoziert ist,
![]() sein muss.
Wir werden später sehen, dass die einfachste Wahl, die sich anbietet -
sein muss.
Wir werden später sehen, dass die einfachste Wahl, die sich anbietet -
![]() - falsch ist: die niedrigste
Potenz, die mit den Experimenten in Einklang ist,
ist
- falsch ist: die niedrigste
Potenz, die mit den Experimenten in Einklang ist,
ist
![]() , wobei wir seit Einstein wissen, dass auch diese Wahl nur eine Näherung für
, wobei wir seit Einstein wissen, dass auch diese Wahl nur eine Näherung für ![]() , mit
(
, mit
(![]() Lichtgeschwindigkeit
Lichtgeschwindigkeit ![]() m/sec) ist. Durch die Einführung der abtstrakten Begriffe
m/sec) ist. Durch die Einführung der abtstrakten Begriffe
![]() und
und
![]() sind wir imstande, das Hamilton Prinzip zu formulieren. Dem Massenpunkt
sind wir imstande, das Hamilton Prinzip zu formulieren. Dem Massenpunkt ![]() ordnen wir die Lagrange
Funktion zu:
ordnen wir die Lagrange
Funktion zu:
![\includegraphics [width=4cm]{f112l.eps}](img196.png)
![\includegraphics [width=4cm]{f112r.eps}](img197.png)
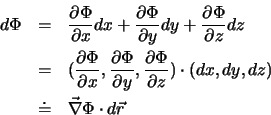
![\begin{eqnarray*}
\int \limits_C \vec F \cdot d \vec r &=&
\int \limits_C \lef...
... \frac{dy}{dt}
+ F_z (t) \frac{dz}{dt} \right ] \, dt
\quad .
\end{eqnarray*}](img233.png)
![]() und die Raumkurve
und die Raumkurve ![]() seien gegeben durch
seien gegeben durch
![]() und
und
![]() . Die von der Kraft geleistete Arbeit zwischen den Zeiten
. Die von der Kraft geleistete Arbeit zwischen den Zeiten ![]() ist
ist
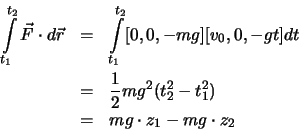
![]() zu einem gegebenenm Endpunkt zur Zeit
zu einem gegebenenm Endpunkt zur Zeit ![]() derart, dass die Wirkung
derart, dass die Wirkung
![]() ist.
ist. ![]() ist hier der sogenannte Variationsparameter, der so gewählt werden muss,
damit
ist hier der sogenannte Variationsparameter, der so gewählt werden muss,
damit ![]() minimal wird. Damit ist
minimal wird. Damit ist
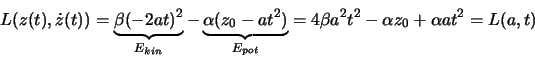
![]() und
und
![]() seien bekannt, dann besagt unser Variationsprinzip, dass
seien bekannt, dann besagt unser Variationsprinzip, dass ![]() von
von ![]() unabhängig ist.
Wir haben damit eine Voraussage produziert, die man experimentell testen kann.
Ist der Test erfolgreich, so freuen wir uns, dass aus einem so abstrakten Prinzip direkt eine
solch konkrete (und gewissermassen überraschende) experimentelle Tatsache folgt.
unabhängig ist.
Wir haben damit eine Voraussage produziert, die man experimentell testen kann.
Ist der Test erfolgreich, so freuen wir uns, dass aus einem so abstrakten Prinzip direkt eine
solch konkrete (und gewissermassen überraschende) experimentelle Tatsache folgt.
![\begin{eqnarray*}
\delta I
&=&
I [ y(x) + \delta y(x)]
-
I [ y (x) ]
\nonu...
...ht )
-
F \left (
x, y (x), y'(x)
\right)\quad \nonumber \\
\end{eqnarray*}](img269.png)
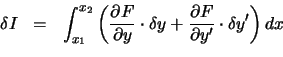
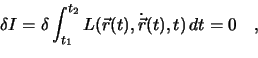
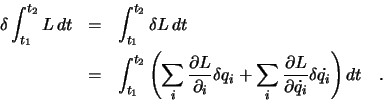
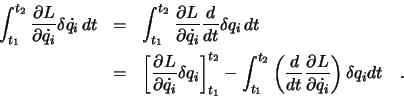
![\begin{displaymath}
\delta I = \int_{t_1}^{t_2} \left[ \sum_i \left(
\frac{\p...
...artial \dot{q_i}}
\right) \delta q_i \right] dt = 0 \quad .
\end{displaymath}](img288.png)
![]() ist die Beschleunigung von
ist die Beschleunigung von ![]() , und beschreibt
die Änderung der Geschwindigkeit. Die negative Ableitung der potentiellen Energie ist die
Kraft, die für die Änderung der Geschwindigkeit verantwortlich ist.
Die Beschleunigung wird in den Einheiten
, und beschreibt
die Änderung der Geschwindigkeit. Die negative Ableitung der potentiellen Energie ist die
Kraft, die für die Änderung der Geschwindigkeit verantwortlich ist.
Die Beschleunigung wird in den Einheiten ![]() gemessen, die Kraft misst man in
gemessen, die Kraft misst man in
![]() . Die Energie ist deshalb
. Die Energie ist deshalb
![]() .
Am Beispiel von Galileo nehmen die BG eine besonders einfache Form an.
Die potentielle Energie, die der Ursprung der Kraft ist, ist bekannterweise
.
Am Beispiel von Galileo nehmen die BG eine besonders einfache Form an.
Die potentielle Energie, die der Ursprung der Kraft ist, ist bekannterweise ![]() .
Die Kraft ist
.
Die Kraft ist
![]() . Die Bewegungsgleichungen lauten
. Die Bewegungsgleichungen lauten