



Nächste Seite: Das Hamilton-Prinzip
Aufwärts: Die Bewegungsgleichungen
Vorherige Seite: Die Bewegungsgleichungen
Inhalt
Einführung
Eine der wichtigsten Erscheinungen der Natur ist die Bewegung.
Bewegt sich ein Objekt über Abstände, die viel grösser als seine Ausdehnung sind,
so kann dieses Objekt als Massenpunkt 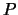 betrachtet werden, d.h. ein geometrischer Punkt
betrachtet werden, d.h. ein geometrischer Punkt 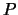 , der eine
Masse
, der eine
Masse 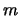 hat, wobei
hat, wobei 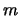 das einzige Merkmal ist, das Massenpunkte voneinander unterscheidet (Einheiten für die Masse:
das einzige Merkmal ist, das Massenpunkte voneinander unterscheidet (Einheiten für die Masse: 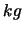 ).
Im Fall eines Massenpunktes kann dann
seine endliche Ausdehnung für die Beschreibung
der Bewegung vernachlässigt werden. Beispielsweise kann man für die Beschreibung
der Umlaufbahn der Erde um die Sonne die Ausdehnung der Erde vernachlässigen -
will man hingegen erklären, warum es Tag und Nacht gibt, muss man berücksichtigen,
dass sich die Erde als Konsequenz ihrer endlichen Ausdehnung um ihre eigene Achse dreht.
Die Lage des Massenpunktes in Bezug auf ein geeignetes Koordinatensystem beschreibt
einen Ortsvektor
).
Im Fall eines Massenpunktes kann dann
seine endliche Ausdehnung für die Beschreibung
der Bewegung vernachlässigt werden. Beispielsweise kann man für die Beschreibung
der Umlaufbahn der Erde um die Sonne die Ausdehnung der Erde vernachlässigen -
will man hingegen erklären, warum es Tag und Nacht gibt, muss man berücksichtigen,
dass sich die Erde als Konsequenz ihrer endlichen Ausdehnung um ihre eigene Achse dreht.
Die Lage des Massenpunktes in Bezug auf ein geeignetes Koordinatensystem beschreibt
einen Ortsvektor 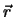 , die Bahn von
, die Bahn von 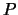 eine Vektorfunktion
eine Vektorfunktion 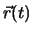 , wobei der reelle Parameter
, wobei der reelle Parameter
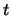 die Zeit ist. (Einheiten für
die Zeit ist. (Einheiten für
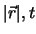 :
: 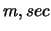 )
)
Verschiedene Grössen in der Physik, wie zum Beispiel die Grundgrössen Länge, Masse
und Zeit, können im Rahmen der Newtonschen Mechanik durch eine einzige reelle
Zahl spezifiziert werden. Diese Zahl kann dabei von dem Einheitensystem abhängen,
in dem wir die Messung vornehmen. Solche Grössen bezeichnen wir als Skalare. Ein
Skalar wird durch einen Buchstaben angegeben, z.B. für die Zeit 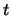 und für die
Masse
und für die
Masse 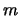 .
.
Abbildung:
Vektor  (links).
(links).
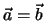 (rechts)
(rechts)
|
|
Andere Grössen in der Physik, wie die Ortsangabe oder die Geschwindigkeit bedürfen
zu ihrer vollständigen Spezifikation der Angabe eines Betrages und einer
Richtung. Solche Grössen nennen wir Vektoren und kennzeichnen sie durch einen
Pfeil über den Buchstaben, um die Bedeutung der Richtungsangabe hervorzuheben.
So schreiben wir beispielsweise für den Ortsvektor 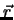 . Ein Vektor verbindet zwei Punkte, beispielsweise
bezeichnen wir den Betrag oder die Länge eines Vektors
. Ein Vektor verbindet zwei Punkte, beispielsweise
bezeichnen wir den Betrag oder die Länge eines Vektors  mit
mit 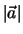 oder
oder 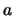 .
Wir wollen nun die einfachen Gesetze der Vektoralgebra behandeln.
Zwei Vektoren
.
Wir wollen nun die einfachen Gesetze der Vektoralgebra behandeln.
Zwei Vektoren  und
und 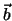 sind gleich, wenn sie den gleichen
Betrag und die gleiche Richtung aufweisen unabhängig von ihrem
Anfangspunkt.
Einen Vektor, der die gleiche Länge wie der Vektor
sind gleich, wenn sie den gleichen
Betrag und die gleiche Richtung aufweisen unabhängig von ihrem
Anfangspunkt.
Einen Vektor, der die gleiche Länge wie der Vektor  aufweist,
aber in die entgegengesetzte Richtung zeigt, bezeichnen wir mit
aufweist,
aber in die entgegengesetzte Richtung zeigt, bezeichnen wir mit 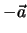 .
Zwei Vektoren
.
Zwei Vektoren  und
und 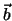 werden addiert, indem man durch
Parallelverschiebung den Fusspunkt des einen Vektors
werden addiert, indem man durch
Parallelverschiebung den Fusspunkt des einen Vektors 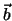 mit der
Pfeilspitze des anderen Vektors
mit der
Pfeilspitze des anderen Vektors  zur Deckung bringt.
zur Deckung bringt.
Abbildung 1.2:
Addition von Vektoren (links) und Kommutativität (rechts)
|
|
Der Summenvektor
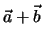 beginnt am Fusspunkt von
beginnt am Fusspunkt von  und reicht bis zur Spitze von
und reicht bis zur Spitze von
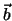 .
.
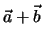 entspricht der Diagonalen des von
entspricht der Diagonalen des von  und
und
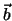 aufgespannten Parallelogramms.
Für die Vektorsumme gilt die
Kommutativität
aufgespannten Parallelogramms.
Für die Vektorsumme gilt die
Kommutativität
Entscheidend für die Kommutativität ist die freie Parallelverschiebbarkeit der
Vektoren.
Assoziativität:
Wiederum überzeugt man sich aufgrund einer graphischen Veranschaulichung sofort
von der Richtigkeit dieser Behauptung.
Abbildung 1.3:
Assoziativität
|
|
Die Differenz zweier Vektoren  und
und 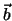 oder die Vektorsubtraktion
ist definiert als
oder die Vektorsubtraktion
ist definiert als
Subtrahiert man  von sich selbst, so ergibt sich der Nullvektor
von sich selbst, so ergibt sich der Nullvektor
Der Nullvektor hat den Betrag 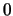 ; er ist richtungslos. Für alle Vektoren gilt
; er ist richtungslos. Für alle Vektoren gilt
Unter dem Produkt 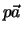 eines Vektors
eines Vektors  mit einem Skalar
mit einem Skalar 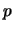 , wobei
, wobei 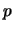 eine reelle Zahl ist, versteht man einen Vektor, der die gleiche Richtung
aufweist wie
eine reelle Zahl ist, versteht man einen Vektor, der die gleiche Richtung
aufweist wie  und den Betrag
und den Betrag
hat.
Abbildung 1.4:
Multiplikation mit einer Zahl
|
|
Hierbei gilt das Distributivgesetz, d. h.
sowie das Assoziativgesetz
Ein Einheitsvektor ist ein Vektor mit der Länge 1. Aus jedem Vektor  lässt sich durch Multiplikation mit dem Kehrwert seines Betrages ein
Einheitsvektor
lässt sich durch Multiplikation mit dem Kehrwert seines Betrages ein
Einheitsvektor 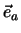 in Richtung von
in Richtung von  konstruieren.
konstruieren.
und damit auch
mit
Einheitsvektoren werden in der Regel mit den Buchstaben 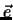 oder
oder 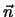 bezeichnet.
Wir fassen die Gesetze der Vektoralgebra zusammen
bezeichnet.
Wir fassen die Gesetze der Vektoralgebra zusammen
-
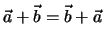 Kommutativgesetz der Addition
Kommutativgesetz der Addition
-
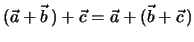 Assoziativgesetz der Addition
Assoziativgesetz der Addition
-
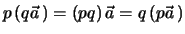 Assoziativgesetz der Multiplikation
Assoziativgesetz der Multiplikation
-
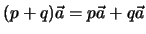 Distributivgesetz
Distributivgesetz
-
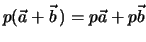 Distributivgesetz
Distributivgesetz
Bislang haben wir Ortsvektoren als einen Spezialfall der Vektoren diskutiert.
Der Zusammenhang mit dem abstrakten mathematischen Vektorbegriff ist leicht
herstellbar. Die Gesamtheit der Vektoren bilden einen linearen Vektorraum 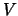 über dem Körper der reellen Zahlen
über dem Körper der reellen Zahlen 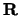 . Es werden die folgenden Axiome erfüllt:
. Es werden die folgenden Axiome erfüllt:
- Zwischen zwei Elementen
 ist eine
Verknüpfung (Addition) definiert
ist eine
Verknüpfung (Addition) definiert
mit
-
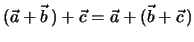
- Nullelement:
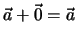 für alle
für alle

- Inverses: Zu jedem
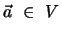 gibt es ein
gibt es ein
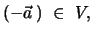 so daß gilt
so daß gilt
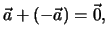
-
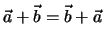 (Kommutativität)
(Kommutativität)
- Multiplikation mit Elementen
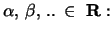
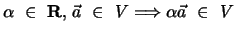
mit
-
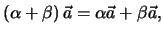
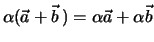 , (Distributivität)
, (Distributivität)
-
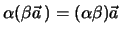 (Assoziativität)
(Assoziativität)
- Es gibt ein Einselement
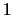 , so dass gilt
, so dass gilt
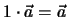 für alle
für alle
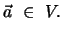
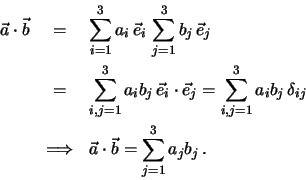
Skalarprodukt von Vektoren.
Wir haben bisher die Multiplikation von Vektoren mit Skalaren betrachtet. Jetzt
wenden wir uns der Multiplikation von Vektoren zu. Hierbei werden wir zwei
unterschiedliche Typen von Produkten von Vektoren kennenlernen, das
Skalarprodukt (inneres Produkt) und das Vektorprodukt (äusseres Produkt).
Als Skalarprodukt zweier Vektoren  und
und
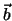 bezeichnet man den folgenden Skalar:
bezeichnet man den folgenden Skalar:
wobei 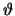 den Winkel zwischen den Vektoren
den Winkel zwischen den Vektoren  und
und 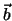 kennzeichnet.
kennzeichnet.
Abbildung 1.5:
Skalarprodukt
|
|
Anschaulich handelt es sich um das Produkt aus der Länge des ersten Vektors mit
der Projektion des zweiten Vektors auf die Richtung des ersten. Offensichtlich
gilt
Basierend auf dieser Einsicht bezeichnen wir zwei Vektoren  und
und 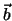 als orthogonal
als orthogonal
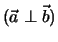 zueinander, falls
zueinander, falls
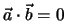
Eine wichtige Eigenschaft des Skalarprodukts betrifft den Betrag eines Vektors.
Wegen
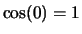 gilt
gilt
Damit können wir schreiben
Für den Einheitsvektor haben wir
Ein Vektorraum, in dem ein Skalarprodukt definiert ist, heisst unitärer
Vektorraum.
Einem Produkt von zwei Vektoren können wir jedoch auch einen Vektor zuordnen.
Das Vektorprodukt (äusseres Produkt, Kreuzprodukt) von zwei Vektoren  und
und
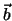 führt zu einem Vektor
führt zu einem Vektor 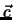
Abbildung 1.6:
Vektorprodukt
|
|
Der Vektor 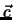 hat folgende Eigenschaften:
hat folgende Eigenschaften:
-
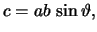
wobei 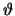 wieder der von
wieder der von  und
und 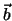 eingeschlossene Winkel
ist. Der Betrag von
eingeschlossene Winkel
ist. Der Betrag von 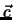 , also
, also 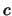 , entspricht dem Flächeninhalt des von
, entspricht dem Flächeninhalt des von
 und
und 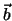 aufgespannten Parallelogramms.
aufgespannten Parallelogramms.
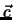 steht senkrecht auf der von
steht senkrecht auf der von  und
und 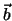 aufgespannten
Ebene.
aufgespannten
Ebene.
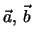 und
und 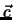 bilden ein Rechtssystem.
bilden ein Rechtssystem.
Wir wollen nun einige wichtige Eigenschaften des Vektorproduktes diskutieren.
- antikommutativ:
-
Für kolineare Vektoren gilt
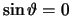 , da
, da
 , und somit verschwindet das Kreuzprodukt.
, und somit verschwindet das Kreuzprodukt.
- distributiv:
- nicht assoziativ
- bilinear
Wir wollen nun einige Eigenschaften von Basisvektoren näher beleuchten. Wir
stellen den Vektor  durch den Einheitsvektor
durch den Einheitsvektor 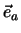 dar, um
Betrags- und Richtungsangabe etwas zu trennen
dar, um
Betrags- und Richtungsangabe etwas zu trennen
Zwei Vektoren  und
und 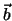 mit der selben Richtung
mit der selben Richtung 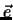 heissen
kolinear. Für sie lassen sich reelle Zahlen
heissen
kolinear. Für sie lassen sich reelle Zahlen
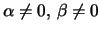 finden, die die Gleichung
finden, die die Gleichung
erfüllen.  und
und 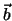 sind linear abhängig. Damit können wir umgedreht
folgende Definition vereinbaren:
sind linear abhängig. Damit können wir umgedreht
folgende Definition vereinbaren:
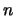 Vektoren
Vektoren
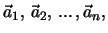 heissen
linear unabhängig, falls die Gleichung
heissen
linear unabhängig, falls die Gleichung
nur durch
erfüllt werden kann. Andernfalls heissen sie linear abhängig.
Ferner gilt die Definition: Die Dimension eines Vektorraumes ist gleich der
maximalen Anzahl linear unabhängiger Vektoren.
In einem 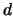 -dimensionalen Vektorraum bildet jede Menge von
-dimensionalen Vektorraum bildet jede Menge von 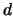 linear unabhängigen
Vektoren eine Basis, d.h. jeder beliebige Vektor dieses Raumes lässt sich als
Linearkombination dieser
linear unabhängigen
Vektoren eine Basis, d.h. jeder beliebige Vektor dieses Raumes lässt sich als
Linearkombination dieser 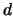 Vektoren beschreiben.
Besonders bedeutsam als Basisvektoren sind Einheitsvektoren, die paarweise
orthogonal zueinander sind. Man spricht in diesem Fall von einem
Orthonormalsystem
Vektoren beschreiben.
Besonders bedeutsam als Basisvektoren sind Einheitsvektoren, die paarweise
orthogonal zueinander sind. Man spricht in diesem Fall von einem
Orthonormalsystem
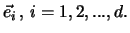 Damit gilt
Damit gilt
mit dem Kronecker-Symbol
Ein Orthonormalsystem, das gleichzeitig Basis des Vektorraumes 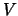 ist,
bezeichnet man als vollständig. Für einen beliebigen Vektor
ist,
bezeichnet man als vollständig. Für einen beliebigen Vektor
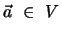 gilt dann
gilt dann
Die 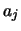 sind die Komponenten des Vektors
sind die Komponenten des Vektors  bezüglich der Basis
bezüglich der Basis
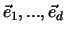 . Beispielsweise bilden die kartesischen Basisvektoren
. Beispielsweise bilden die kartesischen Basisvektoren
 und
und 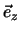 ein vollständiges Orthonormalsystem des
ein vollständiges Orthonormalsystem des
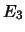 . Die Komponentenschreibweise erlaubt eine gebräuchliche Darstellung des
Vektors als Spaltenvektor:
. Die Komponentenschreibweise erlaubt eine gebräuchliche Darstellung des
Vektors als Spaltenvektor:
oder als Zeilenvektor:
Für den dreidimensionalen euklidischen Raum können wir somit explizit schreiben
oder auch
Mit dem vollständigen Orthonormalsystem können wir auch den Betrag eines Vektors
auswerten. Es ist
Für die Richtungskosinusse erhalten wir mittels der kartesischen Komponenten
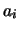
mit

Damit folgt sofort
Ferner bekommen wir
Auch das Skalarprodukt lässt sich mit dem vollständigen Orthonormalsystem leicht
auswerten. Es ist
Wir studieren jetzt Vektorprodukte mit orthonormalen Basisvektoren, die ein
Rechtssystem bilden. Es ist
aber zum Beispiel
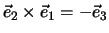 und
und
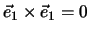 . Multiplizieren wir den resultierenden Vektor
wieder skalar mit
. Multiplizieren wir den resultierenden Vektor
wieder skalar mit 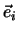 , so folgt
, so folgt
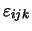 ist das Levi-Civita Symbol oder der sogenannte total
antisymetrische Tensor dritter Stufe. Es ist also
ist das Levi-Civita Symbol oder der sogenannte total
antisymetrische Tensor dritter Stufe. Es ist also
Mit diesem Symbol lassen sich Vektorprodukte der Basisvektoren zusammenfassend
formulieren:
Für allgemeine Vektorprodukte gilt entsprechend
mit der abkürzenden Schreibweise
oder ausführlich
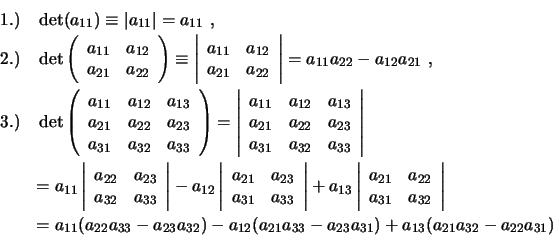
Das Kreuzprodukt lässt sich auch leicht mit Hilfe der Determinantenschreibweise
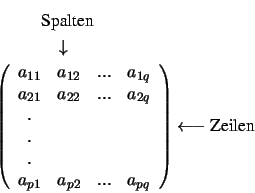
auswerten. Ein rechteckiges Schema von Zahlen wird Matrix genannt.
Der erste Index des Koeffizienten gibt die Zeile an, der zweite die Spalte. Für
den Fall, dass 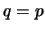 ist, spricht man von einer quadratischen Matrix. Dieser
Matrix lässt sich ein Zahlenwert
ist, spricht man von einer quadratischen Matrix. Dieser
Matrix lässt sich ein Zahlenwert 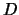 zuordnen, der Determinante genannt wird. Für
die Dimensionen
zuordnen, der Determinante genannt wird. Für
die Dimensionen 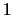 ,
, 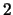 und
und 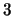 lässt sich dieser Wert folgendermassen auswerten
lässt sich dieser Wert folgendermassen auswerten
Mit Hilfe der Determinantenschreibweise können wir das Vektorprodukt auch formal
auswerten durch
Dies ist identisch mit dem bereits abgeleiteten Resultat.
Wird jedem Wert einer skalaren Variablen 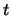 ein Vektor
ein Vektor 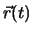 zugeordnet, dann heisst
zugeordnet, dann heisst 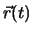 Vektorfunktion der skalaren Variable
Vektorfunktion der skalaren Variable 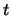 . Trägt man
. Trägt man 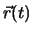 in einem festen Punkt
in einem festen Punkt 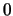 an, dann liegen die Endpunkte
von
an, dann liegen die Endpunkte
von 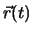 auf einer Raumkurve, die Trajektorie oder die Bahnkurve des Massenpunktes
auf einer Raumkurve, die Trajektorie oder die Bahnkurve des Massenpunktes 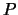 .
.
Abbildung 1.7:
Bahnkurve eines Massenpunktes
|
|
Ein wichtiger Begriff ist die Ableitung derartiger vektorwertiger Funktionen. Wir betrachten 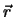 zu verschiedenen
Zeiten
zu verschiedenen
Zeiten 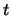 und
und 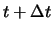 und bilden den Differenzvektor
und bilden den Differenzvektor
 . Dies erlaubt die
Geschwindigkeit als Grenzübergang zu definieren:
. Dies erlaubt die
Geschwindigkeit als Grenzübergang zu definieren:
In einem zeitunabhängigen orthonormalen Basissystem 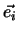 gilt
gilt
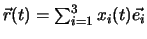 , kurz
, kurz
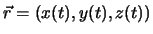 und
und
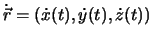 (sog. kartesische Koordinaten). Ein Massenpunkt
(sog. kartesische Koordinaten). Ein Massenpunkt  in einem euklidischen Raum hat dementsprechend 3 Freiheitsgrade, d.h. seine Lage
ist durch die Angabe von 3 Koordinaten eindeutig festgelegt.
Es gelten die folgenden Ableitungsregeln
in einem euklidischen Raum hat dementsprechend 3 Freiheitsgrade, d.h. seine Lage
ist durch die Angabe von 3 Koordinaten eindeutig festgelegt.
Es gelten die folgenden Ableitungsregeln
Höhere Ableitungen einer Vektorfunktion lassen sich entsprechend definieren. Für analytische Vektorfunktionen gilt die Taylor Entwicklung um 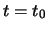 :
:
Die Integration von vektorwertigen Funktionen erfolgt auch komponentenweise:
bei der konkreten Lösung physikalischer Probleme ist die Wahl geeigneter Koordinaten ein sehr wesentlicher Lösungsschritt.
Benutzt man kartesische Koordinaten, dann betrachtet man 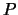 sozusagen als die Ecke eines Parallelepipeds. Man kann
sich aber
sozusagen als die Ecke eines Parallelepipeds. Man kann
sich aber 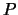 auf einer Kugeloberfläche (Zylinderoberfläche) vorstellen: dann benutzt man Kugelkoordinaten( Zylinderkoordinaten):
auf einer Kugeloberfläche (Zylinderoberfläche) vorstellen: dann benutzt man Kugelkoordinaten( Zylinderkoordinaten):
Abbildung 1.8:
Kugelkoordinaten (links) und Zylinderkoordinaten (rechts)
|
|
Zylinderkoordinaten in der Ebene  heissen auch Polarkoordinaten. Kugel-und Zylinderkoordinaten sind ein Beispiel von
krummlinigen Koordinaten. Mit einer geeigneten Parametrisierung
heissen auch Polarkoordinaten. Kugel-und Zylinderkoordinaten sind ein Beispiel von
krummlinigen Koordinaten. Mit einer geeigneten Parametrisierung
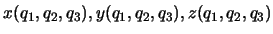 kann man die
krummlinigen Koordinaten
kann man die
krummlinigen Koordinaten 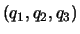 dazu benutzen, den ganzen euklidischen Raum als eine aufeinanderfolgende
Sequenz von Raumflächen zu decken.
dazu benutzen, den ganzen euklidischen Raum als eine aufeinanderfolgende
Sequenz von Raumflächen zu decken.
Der direkteste Weg, die Bewegung von 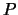 zu erfassen, ist die Messung
von
zu erfassen, ist die Messung
von 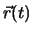 über ein gewisses Zeitintervall. Dadurch lässt sich vielleicht ein
Gesetz erkennen, mit dessen Hilfe man den weiteren Verlauf der Bewegung voraussagen kann.
So haben Naturwissenschaftler bis und mit Galileo Galilei gearbeitet.
Durch unzählige Beobachtungen hatte man ein sehr genaues Bild, z.B. der Dynamik der Planeten
und der Sterne (fast so genau wie unseres) erlangt, und konnte damit schon Begriffe wie die
jährliche Periodizität der Erdbewegung um die Sonne formulieren.
Das Experiment von Galileo auf dem Turm von Pisa ist in diesem Sinne ein Merkmal
in der Geschichte der Physik: Er lässt eine Kugel aus einer Höhe
über ein gewisses Zeitintervall. Dadurch lässt sich vielleicht ein
Gesetz erkennen, mit dessen Hilfe man den weiteren Verlauf der Bewegung voraussagen kann.
So haben Naturwissenschaftler bis und mit Galileo Galilei gearbeitet.
Durch unzählige Beobachtungen hatte man ein sehr genaues Bild, z.B. der Dynamik der Planeten
und der Sterne (fast so genau wie unseres) erlangt, und konnte damit schon Begriffe wie die
jährliche Periodizität der Erdbewegung um die Sonne formulieren.
Das Experiment von Galileo auf dem Turm von Pisa ist in diesem Sinne ein Merkmal
in der Geschichte der Physik: Er lässt eine Kugel aus einer Höhe 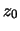 fallen, misst ihre
Lage
fallen, misst ihre
Lage 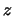 als Funktion der Zeit und schliesst auf ein
als Funktion der Zeit und schliesst auf ein 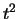 -Gesetz:
-Gesetz:
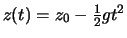 .
Galileo war danach imstande, die Position der Kugel zu jeder Zeit anzugeben.
.
Galileo war danach imstande, die Position der Kugel zu jeder Zeit anzugeben.
Im Prinzip könnte man auf diese Art alle wichtigen Bewegungen der Natur erfassen.
Dank Sir Isaac Newton wissen wir jedoch, dass hinter der Vielfalt von
Bewegungen noch fundamentalere Gesetze existieren, anhand derer die Bahn von 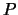 im Prinzip
voraussehbar ist, wenn nur zu einem bestimmten Zeitpunkt Ort und Geschwindigkeit
bekannt sind. Das vereinfacht natürlich das Leben des Physikers: Er muss nicht jeden
im Prinzip
voraussehbar ist, wenn nur zu einem bestimmten Zeitpunkt Ort und Geschwindigkeit
bekannt sind. Das vereinfacht natürlich das Leben des Physikers: Er muss nicht jeden 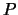 mühsam verfolgen,
um ein empirisches Gesetz zu formulieren. Eine einzige Angabe (
mühsam verfolgen,
um ein empirisches Gesetz zu formulieren. Eine einzige Angabe (
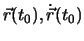 ) genügt.
Diese Angabe nennt man Anfangsbedingungen, die Gesetze, die die Bewegung beschreiben,
nennt man Bewegungsgleichungen.
) genügt.
Diese Angabe nennt man Anfangsbedingungen, die Gesetze, die die Bewegung beschreiben,
nennt man Bewegungsgleichungen.




Nächste Seite: Das Hamilton-Prinzip
Aufwärts: Die Bewegungsgleichungen
Vorherige Seite: Die Bewegungsgleichungen
Inhalt
Kraeutler Vincent
2000-05-30
![\includegraphics [width=4cm]{f11l.eps}](img22.png)
![\includegraphics [width=4cm]{f11r.eps}](img23.png)
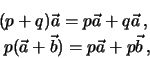
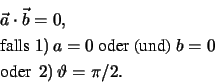
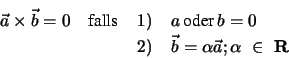
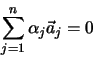
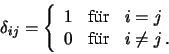
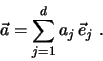
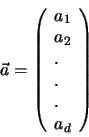
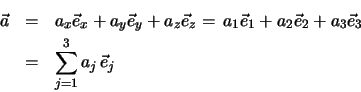
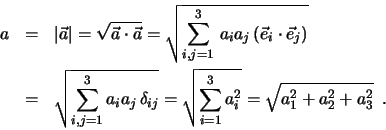
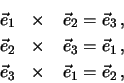
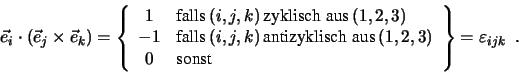
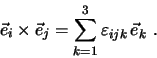
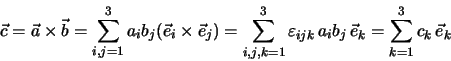
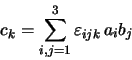

![\begin{eqnarray*}
\frac{d}{dt} [f(t) \, \vec a(t)] &=& \dot{f} (t) \, \vec a (t...
...) \times \vec b(t) +
\vec a(t) \times \dot{\vec b} (t) \quad .
\end{eqnarray*}](img152.png)
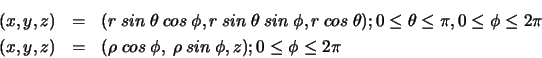
![]() zu erfassen, ist die Messung
von
zu erfassen, ist die Messung
von ![]() über ein gewisses Zeitintervall. Dadurch lässt sich vielleicht ein
Gesetz erkennen, mit dessen Hilfe man den weiteren Verlauf der Bewegung voraussagen kann.
So haben Naturwissenschaftler bis und mit Galileo Galilei gearbeitet.
Durch unzählige Beobachtungen hatte man ein sehr genaues Bild, z.B. der Dynamik der Planeten
und der Sterne (fast so genau wie unseres) erlangt, und konnte damit schon Begriffe wie die
jährliche Periodizität der Erdbewegung um die Sonne formulieren.
Das Experiment von Galileo auf dem Turm von Pisa ist in diesem Sinne ein Merkmal
in der Geschichte der Physik: Er lässt eine Kugel aus einer Höhe
über ein gewisses Zeitintervall. Dadurch lässt sich vielleicht ein
Gesetz erkennen, mit dessen Hilfe man den weiteren Verlauf der Bewegung voraussagen kann.
So haben Naturwissenschaftler bis und mit Galileo Galilei gearbeitet.
Durch unzählige Beobachtungen hatte man ein sehr genaues Bild, z.B. der Dynamik der Planeten
und der Sterne (fast so genau wie unseres) erlangt, und konnte damit schon Begriffe wie die
jährliche Periodizität der Erdbewegung um die Sonne formulieren.
Das Experiment von Galileo auf dem Turm von Pisa ist in diesem Sinne ein Merkmal
in der Geschichte der Physik: Er lässt eine Kugel aus einer Höhe ![]() fallen, misst ihre
Lage
fallen, misst ihre
Lage ![]() als Funktion der Zeit und schliesst auf ein
als Funktion der Zeit und schliesst auf ein ![]() -Gesetz:
-Gesetz:
![]() .
Galileo war danach imstande, die Position der Kugel zu jeder Zeit anzugeben.
.
Galileo war danach imstande, die Position der Kugel zu jeder Zeit anzugeben.
![]() im Prinzip
voraussehbar ist, wenn nur zu einem bestimmten Zeitpunkt Ort und Geschwindigkeit
bekannt sind. Das vereinfacht natürlich das Leben des Physikers: Er muss nicht jeden
im Prinzip
voraussehbar ist, wenn nur zu einem bestimmten Zeitpunkt Ort und Geschwindigkeit
bekannt sind. Das vereinfacht natürlich das Leben des Physikers: Er muss nicht jeden ![]() mühsam verfolgen,
um ein empirisches Gesetz zu formulieren. Eine einzige Angabe (
mühsam verfolgen,
um ein empirisches Gesetz zu formulieren. Eine einzige Angabe (
![]() ) genügt.
Diese Angabe nennt man Anfangsbedingungen, die Gesetze, die die Bewegung beschreiben,
nennt man Bewegungsgleichungen.
) genügt.
Diese Angabe nennt man Anfangsbedingungen, die Gesetze, die die Bewegung beschreiben,
nennt man Bewegungsgleichungen.