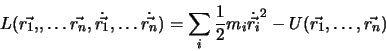Die entscheidende Grösse der Mechanik ist die potentielle Energie. Man fragt sich nun, wie die potentielle Energie beschaffen ist, die in einem bestimmten System von Massenpunkten steckt, (Massen, aber auch Elektronen, Atome, Moleküle und Festkörper!). Diese Frage muss von Fall zu Fall beantwortet werden, und viele Fälle (die potentielle Energie zwischen Quarks, zum Beispiel) sind weit davon entfernt, gelöst zu sein.
Die bis jetzt benutzte Vorstellung über die potentielle Energie,
die aus dem Galileo-Experiment hervorgeht, muss erweitert werden.
Wir hatten nämlich nur mit einem ![]() zu tun. Das ist eine noch zu
begründende Vereinfachung, denn in der Tat sind alle nicht trivialen Probleme der Physik -
seien es die Planeten um die Sonne, sei es die chemische Bindung in Molekülen und Festkörpern -
dadurch gekenngezeichnet, dass mehrere Massenpunkte beteiligt sind. Die potentielle Energie
beschreibt die Wechselwirkung zwischen den Massenpunkten. Diese neue Definition sprengt
natürlich unsere Definition der potentiellen Energie als die Grösse, die in
kinetische Energie umgewandelt wird. Mit dieser Definition können wir jetzt allgemeiner
vorgehen.
zu tun. Das ist eine noch zu
begründende Vereinfachung, denn in der Tat sind alle nicht trivialen Probleme der Physik -
seien es die Planeten um die Sonne, sei es die chemische Bindung in Molekülen und Festkörpern -
dadurch gekenngezeichnet, dass mehrere Massenpunkte beteiligt sind. Die potentielle Energie
beschreibt die Wechselwirkung zwischen den Massenpunkten. Diese neue Definition sprengt
natürlich unsere Definition der potentiellen Energie als die Grösse, die in
kinetische Energie umgewandelt wird. Mit dieser Definition können wir jetzt allgemeiner
vorgehen.
Für die Bestimmung von ![]() gibt es leider kein allgemeines Prinzip.
So hat zum Beispiel Newton das Gravitationsgesetz,
das die Wechselwirkung zwischen zwei Massen beschreibt, aus der Analyse zahlreicher Beobachtungen der Mond- und
Planetenbewegungen (von Tycho Brache und Kepler durchgeführt)
erraten. Seit Newton wissen wir, dass
gibt es leider kein allgemeines Prinzip.
So hat zum Beispiel Newton das Gravitationsgesetz,
das die Wechselwirkung zwischen zwei Massen beschreibt, aus der Analyse zahlreicher Beobachtungen der Mond- und
Planetenbewegungen (von Tycho Brache und Kepler durchgeführt)
erraten. Seit Newton wissen wir, dass
Die Grösse ![]() kann man den
astronomischen Beobachtungen nicht entnehmen, solange man die Masse nicht genau kennt.
Das Gravitationsgesetz lässt sich jedoch mit Massen der Grössenordnung
kann man den
astronomischen Beobachtungen nicht entnehmen, solange man die Masse nicht genau kennt.
Das Gravitationsgesetz lässt sich jedoch mit Massen der Grössenordnung ![]() im Laboratorium prüfen, und auf diese Weise bestimmen. Das Experiment zur Bestimmung von
im Laboratorium prüfen, und auf diese Weise bestimmen. Das Experiment zur Bestimmung von
![]() wurde erstmals von Henry Cavendish im Jahre 1798 durchgeführt,
mit einer Drehwaage.
wurde erstmals von Henry Cavendish im Jahre 1798 durchgeführt,
mit einer Drehwaage.
Aus der Definition der Kraft lässt sich die potentielle Energie angeben:
Die Konstante wird üblicherweise mit ![]() bezeichnet, da sie für die Bewegung
unwesentlich ist (lediglich die Ableitung der potentiellen Energie ist wichtig,
aber beim Ableiten verschwinden die Konstanten). Diese Wahl der Konstante entspricht einer potentiellen Energie, die im Unendlichen verschwindet.
bezeichnet, da sie für die Bewegung
unwesentlich ist (lediglich die Ableitung der potentiellen Energie ist wichtig,
aber beim Ableiten verschwinden die Konstanten). Diese Wahl der Konstante entspricht einer potentiellen Energie, die im Unendlichen verschwindet.
Was hat dieser Ausdruck der potentiellen Energie mit der uns bekannten Formel
![]() zu tun? Um diese Verbindung herzustellen, betrachten wir eine
kleine Masse
zu tun? Um diese Verbindung herzustellen, betrachten wir eine
kleine Masse ![]() in der Nähe einer riesigen Kugel mit dem Radius
in der Nähe einer riesigen Kugel mit dem Radius ![]() und der
riesigen Masse
und der
riesigen Masse ![]() . Dieses Gebilde soll einen Massenpunkt in der Nähe der Erde darstellen.
Wir simulieren dieses System, indem wir die Erde auf einen Punkt schrumpfen lassen,
und
. Dieses Gebilde soll einen Massenpunkt in der Nähe der Erde darstellen.
Wir simulieren dieses System, indem wir die Erde auf einen Punkt schrumpfen lassen,
und ![]() auf den Abstand
auf den Abstand ![]() legen,
legen, ![]() . Dann ist die potentielle Energie
. Dann ist die potentielle Energie
![\begin{eqnarray*}
E_{pot}=-\gamma\frac{Mm}{R+z}+Konst.=-\gamma\frac{Mm}{R(1+\fra...
...Konst. +\gamma\frac{M}{R^2}mz=m[\frac{m\gamma}{R^2}]z + Konst.'
\end{eqnarray*}](img311.png)