



Nächste Seite: Die Wellengleichung
Aufwärts: Schwingungen
Vorherige Seite: Erzwungene Schwingung
Inhalt
Die lineare schwingende Kette
Mit unserem mechanischen Modell konnten wir die Schwingungen von einfachen zweiatomigen Molekülen erfassen, die
entlang einer Koordinate stattfinden. In diesem Modell wurden die Bestandteile der Moleküle durch eine "Feder" gekoppelt,
mit der Federkonstante 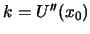 . Wir wollen jetzt mit dem gleichen Federmodell versuchen, Kristallschwingungen
zu beschreiben. Dazu betrachten wir entlang der
. Wir wollen jetzt mit dem gleichen Federmodell versuchen, Kristallschwingungen
zu beschreiben. Dazu betrachten wir entlang der 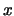 -Koordinate eine lineare Kette von
-Koordinate eine lineare Kette von 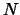 Atomen der Masse
Atomen der Masse 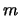 , die
paarweise mit der Federkonstante
, die
paarweise mit der Federkonstante 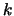 gekoppelt sind. Wir bezeichnen als
gekoppelt sind. Wir bezeichnen als
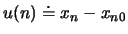 die Abweichung der
die Abweichung der
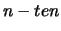 Masse aus der Ruhelage
Masse aus der Ruhelage
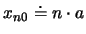 , wobei
, wobei 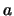 die Gitterkonstante ist.
Die Lagrange Funktion
die Gitterkonstante ist.
Die Lagrange Funktion
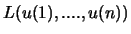 dieses Systems lautet
dieses Systems lautet
Die BG für die 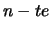 Masse lautet
Masse lautet
Da die Auslenkungen 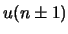 in der BG für das
in der BG für das 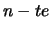 Atom auftreten, bilden alle BG ein System von
Atom auftreten, bilden alle BG ein System von 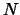 gekoppelten DG. Die Lösung hängt davon ab, welche Randbedingungen der Kette auferlegt werden. Man kann
z.B. die Randatome festhalten oder frei geben. Wenn
gekoppelten DG. Die Lösung hängt davon ab, welche Randbedingungen der Kette auferlegt werden. Man kann
z.B. die Randatome festhalten oder frei geben. Wenn 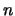 eine kleine Zahl ist, hängen die Lösungen stark von
diesen Randbedingungen ab, wie man am Bsp.
eine kleine Zahl ist, hängen die Lösungen stark von
diesen Randbedingungen ab, wie man am Bsp.  sofort klar ersieht.
Bei einer makroskopischen Anzahl
sofort klar ersieht.
Bei einer makroskopischen Anzahl 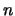 muss der Einfluss der Randbedingungen auf die Schwingungsfrequenzen
klein sein. Physikalisch kann man sich vorstellen, dass die Kette zu einem Kreis gebogen
wird, wobei am
muss der Einfluss der Randbedingungen auf die Schwingungsfrequenzen
klein sein. Physikalisch kann man sich vorstellen, dass die Kette zu einem Kreis gebogen
wird, wobei am 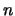 Atom noch eine Feder angebracht ist, die es mit dem ersten Atom verbindet. Damit hat man den
Rand eliminiert. Mathematisch bedeutet diese Biegung der Kette zu einem Kreis die Annahme periodischer (in der
Fachliteratur auch Born-von Karman) Randbedingungen:
Atom noch eine Feder angebracht ist, die es mit dem ersten Atom verbindet. Damit hat man den
Rand eliminiert. Mathematisch bedeutet diese Biegung der Kette zu einem Kreis die Annahme periodischer (in der
Fachliteratur auch Born-von Karman) Randbedingungen: 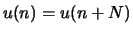 . Die Lösungen des DG Systems mit diesen
Randbedingungen sind solche, die der Realität näher kommen sollten, weil sie Oberflächeneffekte auf die
Festkörpereigenschaften eliminieren.
Zur Lösung des DG Systems macht man den Ansatz
. Die Lösungen des DG Systems mit diesen
Randbedingungen sind solche, die der Realität näher kommen sollten, weil sie Oberflächeneffekte auf die
Festkörpereigenschaften eliminieren.
Zur Lösung des DG Systems macht man den Ansatz
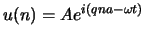 , wobei der Faktor
, wobei der Faktor 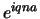 die
die 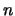 Abhängigkeit der Auslenkung berücksichtigt. Durch Einsetzen des Ansatzes finden wir die charakteristische
Gleichung
Abhängigkeit der Auslenkung berücksichtigt. Durch Einsetzen des Ansatzes finden wir die charakteristische
Gleichung
deren Lösung die möglichen Eigenfrequenzen der schwingenden Kette ergibt.
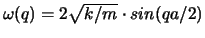 .
Die Randbedingung bestimmt die möglichen Werte vom Parameter
.
Die Randbedingung bestimmt die möglichen Werte vom Parameter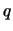 :
:
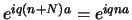 , d.h.
, d.h. 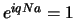 oder
oder
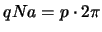 ,
,
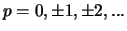 . Die möglichen Schwingungszustände sind durch dicht nebeneinanderliegende
. Die möglichen Schwingungszustände sind durch dicht nebeneinanderliegende
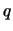 -Werte klassifiziert, jeder
-Werte klassifiziert, jeder 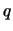 Wert trägt eine bestimmte Eigenfrequenz. Die gesuchten
Wert trägt eine bestimmte Eigenfrequenz. Die gesuchten 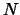 linear unabhängigen
Lösungen können durch die
linear unabhängigen
Lösungen können durch die 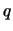 Werte im Intervall
Werte im Intervall 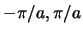 dargestellt werden.
Die Kopplung bewirkt, dass sich die Frequenz
dargestellt werden.
Die Kopplung bewirkt, dass sich die Frequenz 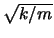 des ungekoppelten Oszillators zu einem Frequenzband
verbreitet. Jeder Frequenz kann ein
des ungekoppelten Oszillators zu einem Frequenzband
verbreitet. Jeder Frequenz kann ein 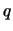 Wert zugeordnet werden. Die
Wert zugeordnet werden. Die 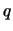 Abhängigkeit von
Abhängigkeit von 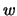 nennt man
Dispersionsrelation. Die Eigenmoden, die zu den Eigenfrequenzen gehören, nennt man Phononen.
Besteht die Kette aus Atomen mit unterschiedlichen alternierenden Massen, erwartet man mindestens
zwei-Phononenbänder, die evtl. durch eine Lücke getrennt sind. Verbindungen wie
nennt man
Dispersionsrelation. Die Eigenmoden, die zu den Eigenfrequenzen gehören, nennt man Phononen.
Besteht die Kette aus Atomen mit unterschiedlichen alternierenden Massen, erwartet man mindestens
zwei-Phononenbänder, die evtl. durch eine Lücke getrennt sind. Verbindungen wie 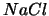 haben
zum Beispiel zwei Phononenbänder: Das untere
Band nennt man akustische Phononen, das obere sind die optischen Phononen. Einen optischen
und akustischen Zweig bekommt man auch, wenn die Kraftkonstanten alternierend sind.
Diese Resultate lassen sich auf dreidimensionale Kristalle erweitern. In drei Dimensionen, wird
haben
zum Beispiel zwei Phononenbänder: Das untere
Band nennt man akustische Phononen, das obere sind die optischen Phononen. Einen optischen
und akustischen Zweig bekommt man auch, wenn die Kraftkonstanten alternierend sind.
Diese Resultate lassen sich auf dreidimensionale Kristalle erweitern. In drei Dimensionen, wird 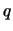 zu einem Vektor, der innerhalb eines Polyeders verteilt ist. Die Phononendispersionsrelationen können
richtungsabhängig werden und einen komplizierteren Verlauf zeigen.
zu einem Vektor, der innerhalb eines Polyeders verteilt ist. Die Phononendispersionsrelationen können
richtungsabhängig werden und einen komplizierteren Verlauf zeigen.




Nächste Seite: Die Wellengleichung
Aufwärts: Schwingungen
Vorherige Seite: Erzwungene Schwingung
Inhalt
Kraeutler Vincent
2000-05-30
![\includegraphics [width=12cm]{f414.eps}](img675.png)