



Nächste Seite: Über dieses Dokument ...
Aufwärts: Schwingungen
Vorherige Seite: Die lineare schwingende Kette
Inhalt
Die Wellengleichung
Wir betrachten Phononen mit 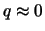 . Für solche Phononen ist die charakteristische Länge
. Für solche Phononen ist die charakteristische Länge
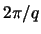 über welche
über welche 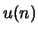 variiert viel grösser als die Gitterkonstante. Wir können daher
variiert viel grösser als die Gitterkonstante. Wir können daher 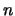 als kontinuierliche Variable
als kontinuierliche Variable 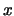 bezeichnen und die BG für
bezeichnen und die BG für 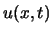 folgendermassen aufstellen:
folgendermassen aufstellen:
Die Materialkonstante
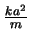 wird als
wird als 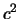 bezeichnet. Ihre Bedeutung wird bald klar.
Diese Gleichung ist die eindimensionale Wellengleichung für die Auslenkung
bezeichnet. Ihre Bedeutung wird bald klar.
Diese Gleichung ist die eindimensionale Wellengleichung für die Auslenkung 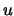 an der Stelle
an der Stelle
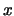 zur Zeit
zur Zeit 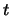 . Die linear unabhängigen Eigenmoden
. Die linear unabhängigen Eigenmoden
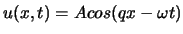 und
und
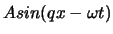 sind spezielle Lösungen der Wellengleichung
und sind ein spezielles Beispiel von Wellen: sie heissen harmonische Wellen. Die allgemeinste
Form der linear unabhängigen Lösungen der eindimensionalen WG ist
sind spezielle Lösungen der Wellengleichung
und sind ein spezielles Beispiel von Wellen: sie heissen harmonische Wellen. Die allgemeinste
Form der linear unabhängigen Lösungen der eindimensionalen WG ist
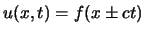 (d' Alembertsche
Lösungen) und die allgemeinste Lösung ist die lineare Superposition der beiden Grundlösungen.
Man stelle sich eine lokale Störung
(d' Alembertsche
Lösungen) und die allgemeinste Lösung ist die lineare Superposition der beiden Grundlösungen.
Man stelle sich eine lokale Störung 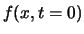 vor, die zum Beispiel ein Maximum bei
vor, die zum Beispiel ein Maximum bei 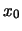 besitzt.
Eine solche Störung kann zum Beispiel eine Verschiebung
der Teilchen eines Mediums aus ihrer Ruhelage (Phononen, Seilwellen, Wasseroberflächenwellen) oder einer
Dichteschwankung bei elastischen Wellen, Schallwellen und Erdbebenwellen bedeuten. Es kann aber ein
von elekromagnetischen Feldern (Licht) bedeuten, das sich durch ein plötzliches Ein- und Ausschalten eines
Stromes gebildet hat.
Wenn diese Störung nach der Wellengleichung evolviert, dann ist die funktionelle Abhängigkeit zur
Zeit
besitzt.
Eine solche Störung kann zum Beispiel eine Verschiebung
der Teilchen eines Mediums aus ihrer Ruhelage (Phononen, Seilwellen, Wasseroberflächenwellen) oder einer
Dichteschwankung bei elastischen Wellen, Schallwellen und Erdbebenwellen bedeuten. Es kann aber ein
von elekromagnetischen Feldern (Licht) bedeuten, das sich durch ein plötzliches Ein- und Ausschalten eines
Stromes gebildet hat.
Wenn diese Störung nach der Wellengleichung evolviert, dann ist die funktionelle Abhängigkeit zur
Zeit 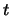
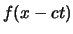 , siehe Figur, d.h. die Störung sieht genau gleich aus wie zur Zeit
, siehe Figur, d.h. die Störung sieht genau gleich aus wie zur Zeit  aber ist am Ort
aber ist am Ort 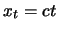 zentriert: die Wellengleichung hat die Störung fortgepflanzt, und zwar mit Beibehaltung der Form. Die
Materialkonstante
zentriert: die Wellengleichung hat die Störung fortgepflanzt, und zwar mit Beibehaltung der Form. Die
Materialkonstante 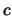 ist die Fortpflanzungsgeschwindigkeit. Die Lösung
ist die Fortpflanzungsgeschwindigkeit. Die Lösung 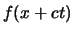 beschreibt eine Welle,
die sich nach rechts entlang der
beschreibt eine Welle,
die sich nach rechts entlang der 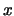 -Achse fortpflanzt.
Die Materialkonstanten, die
-Achse fortpflanzt.
Die Materialkonstanten, die 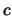 bestimmen, hängen von der Wellenart ab. Bei Phononen ist die zweite
Ableitung der potentiellen Energie massgebend (zusammen mit Masse und Gitterkonstante). Schreiben wir
bestimmen, hängen von der Wellenart ab. Bei Phononen ist die zweite
Ableitung der potentiellen Energie massgebend (zusammen mit Masse und Gitterkonstante). Schreiben wir
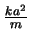 als
als
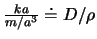 , mit (
, mit (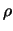 : Dichte) und
: Dichte) und 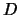 : Zugkraft) dann bekommen
wir die Geschwindigkeit von Seilwellen. Bei Schallwellen ist
: Zugkraft) dann bekommen
wir die Geschwindigkeit von Seilwellen. Bei Schallwellen ist
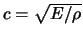 ,
, 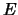 : Elastizitätsmodul. Für
Lichtwellen ist
: Elastizitätsmodul. Für
Lichtwellen ist 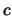 die Lichtgeschwindigkeit.
die Lichtgeschwindigkeit.
Beispiele von Wellen
Beispiel 1. Harmonische Welle.
Die harmonische Welle
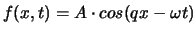 erfüllt die WG, wenn
erfüllt die WG, wenn 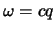 .
Diese ist die Dispersionsrelation, die
wir für langwellige Phononen aus der exakten Lösung erwartet haben. Eine instantane Aufnahme einer harmonischen
Welle erlaubt, die verschiedenen Parameter zu veranschaulichen:
.
Diese ist die Dispersionsrelation, die
wir für langwellige Phononen aus der exakten Lösung erwartet haben. Eine instantane Aufnahme einer harmonischen
Welle erlaubt, die verschiedenen Parameter zu veranschaulichen:
Abbildung 4.10:
Harmonische Welle zu einer festen Zeit (links) und an einem bestimmten Ort (rechts)
|
|
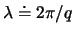 ist der Abstand zweier Wellentäler (oder analoge Punkte der Welle) und heisst Wellenlänge.
ist der Abstand zweier Wellentäler (oder analoge Punkte der Welle) und heisst Wellenlänge.
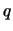 ist die Wellenzahl und gibt gerade die Zahl der Wellentäler pro Längeneinheit an.
Man betrachte jetzt den zeitlichen Ablauf an einem festen Ort,
Nach der Zeit
ist die Wellenzahl und gibt gerade die Zahl der Wellentäler pro Längeneinheit an.
Man betrachte jetzt den zeitlichen Ablauf an einem festen Ort,
Nach der Zeit 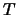 wiederholt sich in
wiederholt sich in 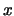 dieselbe Phase der Welle, z.B. ein Wellental:
dieselbe Phase der Welle, z.B. ein Wellental: 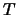 ist die Periode der Welle.
ist die Periode der Welle.
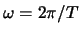 ist dann die Frequenz, mit welcher sich dieselbe Phase pro Zeiteinheit wiederholt. Es gilt:
ist dann die Frequenz, mit welcher sich dieselbe Phase pro Zeiteinheit wiederholt. Es gilt:  .
.
Beispiel 2: Stehende Welle.
Eine von links einfallende harmonische Seilwelle
trifft auf eine feste Halterung (aber es kann sich auch um eine ebene Lichtwelle handeln, die an einem Spiegel reflektiert ist) bei x = 0.
Die Gesamtwelle setzt sich aus der einfallenden und der reflektierten Welle zusammen, wobei die Randbedingung
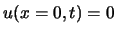
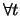 erfüllt werden muss. Die gesuchte Lösung ist
erfüllt werden muss. Die gesuchte Lösung ist
Wie die Figur zeigt, ist das keine normale laufende Welle mehr: Es gibt nämlich Schwingungsknoten, an denen die
Welle überall verschwindet, und es gibt Schwingungszeiten an denen die Auslenkung immer verschwindet. Da die
Schwingungsknoten eine feste Lage im Raum haben, spricht man von einer stehenden Welle.
Die Schwingungsknoten sind durch die Gleichung 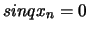 bestimmt, d.h.
bestimmt, d.h.
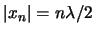 ,
,
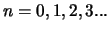 .
.
Abbildung 4.11:
Stehende Welle (links) und Resonator (rechst)
|
|
Beipiel 3: Eigenfrequenzen eines schwingenden Seils.
Hält man das Seil auch noch im Abstand L fest, so tritt die zusätzliche Randbedingung 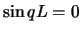 auf, die nur
für bestimmte
auf, die nur
für bestimmte 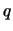 - Zahlen (d.h. für bestimmte Wellenlängen) erfüllbar ist:
- Zahlen (d.h. für bestimmte Wellenlängen) erfüllbar ist:
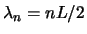 ,
, 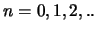 . Dies bedeutet, dass die stehende Welle im Gebiet
. Dies bedeutet, dass die stehende Welle im Gebiet 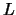 nur
bestimmte Frequenzen
nur
bestimmte Frequenzen
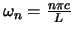 annehmen darf.
Nur solche Wellen, die diese Frequenz haben, können im Gebiet
annehmen darf.
Nur solche Wellen, die diese Frequenz haben, können im Gebiet 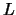 zu beträchtlichen Amplituden schwingen.
Daraus sieht man, dass stehende Wellen fast allen Musikinstrumenten zugrunde liegen: es ist damit möglich,
bestimmte Noten zu selektieren.
Wenn wir an Licht denken, das zwischen zwei Spiegeln reflektiert wird, so können wir uns genauso vorstellen,
dass nur bestimmte Frequenzen und Wellenlängen zwischen den zwei Spiegeln existieren können. In diesem
Fall spricht man von einem optischen Resonator. Ein solcher optischer Resonator ist eine fundamentale Komponente
für die Erzeugung von Laserlicht, die sehr genau monokromatisch ist.
Beipiel 4: Polarisation einer Welle.
zu beträchtlichen Amplituden schwingen.
Daraus sieht man, dass stehende Wellen fast allen Musikinstrumenten zugrunde liegen: es ist damit möglich,
bestimmte Noten zu selektieren.
Wenn wir an Licht denken, das zwischen zwei Spiegeln reflektiert wird, so können wir uns genauso vorstellen,
dass nur bestimmte Frequenzen und Wellenlängen zwischen den zwei Spiegeln existieren können. In diesem
Fall spricht man von einem optischen Resonator. Ein solcher optischer Resonator ist eine fundamentale Komponente
für die Erzeugung von Laserlicht, die sehr genau monokromatisch ist.
Beipiel 4: Polarisation einer Welle.
In der Phononenwelle, die wir zur Herleitung der Wellengleichung benutzt haben, schwingen die Atome entlang
der Ausbreitungsrichtung. Eine solche Welle ist eine longitudinale Welle, d.h. sie ist longitudinal polarisiert.
Es ist aber auch möglich, dass die Störung senkrecht zur Ausbreitungsrichtung stattfindet (Seilwelle und transversale Phononen):
man spricht daher bei der Seilwelle von einer transversalen Polarisation. Dieselbe Polarisation haben EM Wellen,
bei welchen E und B ebenso senkrecht zur Fortpflanzungsrichtung schwingen. Ein weiteres Beispiel einer
longitudinal polarisierten Welle sind Schallwellen. Schall oder elastische Wellen in einem Stab, entstehen indem
eine mikroskopische Menge von Atomen - etwa auf einer Ebene liegend - komprimiert wird. Es bildet
sich in einem Volumenelement ein Überdruck, der die darausfolgende
Menge von Atomen nach vorn befördert. Wie ein Domino breitet sich die ursprüngliche Kompression aus.
Diese Kompression besteht aus einer Auslenkung der Atome aus ihrer Ruhelage, und zwar parallel zur
Ausbreitungsrichtung. Schallwellen sind daher longitudinal polarisiert.
Beipiel 5: Die Ausbreitung von Wellen in drei Dimensionen.
Die Grundlage für die Ausbreitung von Wellen im dreidimensionalen Koordinatenraum ist die dreidimensionale
Wellengleichung
Eine sehr wichtige Lösung dieser Gleichung ist die ebene harmonische Welle
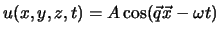 ,
mit
,
mit
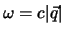 .
.
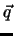 ist der Wellenvektor. Alle Punkte
ist der Wellenvektor. Alle Punkte 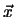 mit gleicher Auslenkung oder Phase liegen auf Ebenen mit der Gleichung
mit gleicher Auslenkung oder Phase liegen auf Ebenen mit der Gleichung
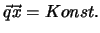 Das sind Ebenen senkrecht zur Ausbreitungsrichtung, die von
Das sind Ebenen senkrecht zur Ausbreitungsrichtung, die von 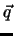 festgelegt ist. Neben den
ebenen Wellen treten in der Physik zuweilen auch Wellen mit gekrümmten Flächen gleicher Phase auf, wie zum Beispiel
Zylinder- oder Kugelwellen. Eine Kugelwelle, zum Beispiel, ist eine Welle, die einen kugelförmigen Wellenfront besitzt.
Kugelwellen breiten sich typischerweise aus einer Punktquelle aus. Die allgemeine Form einer Kugelwelle, die sich vom
Ursprung des Koordinatensystems mit Fortpflanzungsgeschwindigkeit c ausbreitet, finden wir als die Lösung der
radialsymmetrischen Wellengleichung
festgelegt ist. Neben den
ebenen Wellen treten in der Physik zuweilen auch Wellen mit gekrümmten Flächen gleicher Phase auf, wie zum Beispiel
Zylinder- oder Kugelwellen. Eine Kugelwelle, zum Beispiel, ist eine Welle, die einen kugelförmigen Wellenfront besitzt.
Kugelwellen breiten sich typischerweise aus einer Punktquelle aus. Die allgemeine Form einer Kugelwelle, die sich vom
Ursprung des Koordinatensystems mit Fortpflanzungsgeschwindigkeit c ausbreitet, finden wir als die Lösung der
radialsymmetrischen Wellengleichung
Das ergibt:
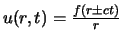 , wie durch direktes Einsetzen sichtbar wird.
Vergessen wir für einen Augenblick den Faktor r im Nenner. Die Amplitude der Welle zu einer bestimmten Zeit hat dann als
Funktion des Abstands vom Ursprung eine bestimmte Gestalt, die mit der Geschwindigkeit c vom Ursprung ausläuft
(oder zum Ursprung hinläuft). Der Faktor r im Nenner sagt uns aber, daß die Amplitude der Welle im Lauf der Ausbreitung
proportional zu 1/r abnimmt. Mit anderen Worten: Während bei einer ebenen Welle die Amplitude während des
Ausbreitungsvorgangs konstant bleibt, nimmt die Amplitude einer Kugelwelle stetig ab, wie es in der Figur dargestellt ist.
Beipiel 6: Akustische Wellen in der Geologie.
Die Erde kann zu Eigenschwingungen angeregt werden, insbesondere bei Erdbeben.
Die Grundschwingungsperiode beträgt rund 50 Minuten, was etwa der Zeit eines akustischen Hin- und Rücklaufs durch die Erde entspricht.
Das Bild zeigt die Deformation der Erde (nicht massstabgetreu) bei einer solchen Schwingung zur Zeit
t = 0 und 25 min später.
Akustische Wellen sind aber auch ein leistungsfähiges Hilfsmittel zur Untersuchung des Erdinnern.
Unsere Kenntnis vom Erdinnern stammt hauptsächlich von seismologischen Beobachtungen.
Aus der Reisezeit und Reiseroute von Erdbebenwellen kann man den radialen Verlauf der
Schallgeschwindigkeit im Erdinnern bestimmen: Das Bild zeigt z.B. die longitudinalen und
transversalen Schallgeschwindigkeiten im Erdinnern. Deutlich sichtbar ist das Nullwerden der
transversalen Geschwindigkeit und damit der Schersteifigkeit im Erdinnern, welches auf den flüssigen
Zustand des Erdkerns hinweist.
Die akustische Information zeigt aber nicht nur die Existenz und Abmessung des flüssigen Erdkerns,
sondern darüber hinaus weitere Unstetigkeiten, auf die wir hier nur hinweisen wollen. (Zum Beispiel die mit
F bezeichnete Unstetigkeit in 5 200 km Tiefe, welche eine weitere Phasenänderung flüssig - fest innerhalb
des Erdkerns andeutet.)
, wie durch direktes Einsetzen sichtbar wird.
Vergessen wir für einen Augenblick den Faktor r im Nenner. Die Amplitude der Welle zu einer bestimmten Zeit hat dann als
Funktion des Abstands vom Ursprung eine bestimmte Gestalt, die mit der Geschwindigkeit c vom Ursprung ausläuft
(oder zum Ursprung hinläuft). Der Faktor r im Nenner sagt uns aber, daß die Amplitude der Welle im Lauf der Ausbreitung
proportional zu 1/r abnimmt. Mit anderen Worten: Während bei einer ebenen Welle die Amplitude während des
Ausbreitungsvorgangs konstant bleibt, nimmt die Amplitude einer Kugelwelle stetig ab, wie es in der Figur dargestellt ist.
Beipiel 6: Akustische Wellen in der Geologie.
Die Erde kann zu Eigenschwingungen angeregt werden, insbesondere bei Erdbeben.
Die Grundschwingungsperiode beträgt rund 50 Minuten, was etwa der Zeit eines akustischen Hin- und Rücklaufs durch die Erde entspricht.
Das Bild zeigt die Deformation der Erde (nicht massstabgetreu) bei einer solchen Schwingung zur Zeit
t = 0 und 25 min später.
Akustische Wellen sind aber auch ein leistungsfähiges Hilfsmittel zur Untersuchung des Erdinnern.
Unsere Kenntnis vom Erdinnern stammt hauptsächlich von seismologischen Beobachtungen.
Aus der Reisezeit und Reiseroute von Erdbebenwellen kann man den radialen Verlauf der
Schallgeschwindigkeit im Erdinnern bestimmen: Das Bild zeigt z.B. die longitudinalen und
transversalen Schallgeschwindigkeiten im Erdinnern. Deutlich sichtbar ist das Nullwerden der
transversalen Geschwindigkeit und damit der Schersteifigkeit im Erdinnern, welches auf den flüssigen
Zustand des Erdkerns hinweist.
Die akustische Information zeigt aber nicht nur die Existenz und Abmessung des flüssigen Erdkerns,
sondern darüber hinaus weitere Unstetigkeiten, auf die wir hier nur hinweisen wollen. (Zum Beispiel die mit
F bezeichnete Unstetigkeit in 5 200 km Tiefe, welche eine weitere Phasenänderung flüssig - fest innerhalb
des Erdkerns andeutet.)




Nächste Seite: Über dieses Dokument ...
Aufwärts: Schwingungen
Vorherige Seite: Die lineare schwingende Kette
Inhalt
Kraeutler Vincent
2000-05-30
![\begin{eqnarray*}
m\frac{\partial^2 u}{\partial t^2}& = & k[u(n-1,t)+ u(n+1,t)]...
...ial t^2}& = & \frac{k a^2}{m} \frac{\partial^2 u}{\partial x^2}
\end{eqnarray*}](img703.png)
![\begin{eqnarray*}
m\frac{\partial^2 u}{\partial t^2}& = & k[u(n-1,t)+ u(n+1,t)]...
...ial t^2}& = & \frac{k a^2}{m} \frac{\partial^2 u}{\partial x^2}
\end{eqnarray*}](img703.png)
![]() erfüllt die WG, wenn
erfüllt die WG, wenn ![]() .
Diese ist die Dispersionsrelation, die
wir für langwellige Phononen aus der exakten Lösung erwartet haben. Eine instantane Aufnahme einer harmonischen
Welle erlaubt, die verschiedenen Parameter zu veranschaulichen:
.
Diese ist die Dispersionsrelation, die
wir für langwellige Phononen aus der exakten Lösung erwartet haben. Eine instantane Aufnahme einer harmonischen
Welle erlaubt, die verschiedenen Parameter zu veranschaulichen:
![\begin{eqnarray*}
u(x,t) & = & A [\cos(\omega t - qx) -\cos(\omega t + qx)]\\
& = & 2A \sin qx \sin \omega t
\end{eqnarray*}](img726.png)
![\includegraphics [width=10cm]{f424.eps}](img736.png)
![\includegraphics [width=10cm]{f428.eps}](img744.png)
![\includegraphics[width=6cm]{f425.eps}](img746.png)
![\includegraphics[width=10cm]{f426.eps}](img747.png)
![\includegraphics[width=10cm]{f427.eps}](img748.png)