



Nächste Seite: Die lineare schwingende Kette
Aufwärts: Schwingungen
Vorherige Seite: Eindimensionale harmonische Schwingung
Inhalt
Erzwungene Schwingung
Wir gehen nun zur Betrachtung von Schwingungen eines Systems über,
auf das ein äusseres veränderliches Feld wirkt. Derartige Schwingungen heissen
erzwungene Schwingungen im Gegensatz zu den im vorherigen Paragraphen untersuchten
freien Schwingungen.
Bei der Anwesenheit eines äusseren Feldes besitzt das System neben der eigenen
potentiellen Energie 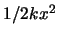 ausserdem die potentielle Energie
ausserdem die potentielle Energie 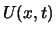 ,
die von der Wirkung des äusseren Feldes herrührt. Wenn wir dieses Zusatzglied in einer
Potenzreihe von der kleinen Grösse
,
die von der Wirkung des äusseren Feldes herrührt. Wenn wir dieses Zusatzglied in einer
Potenzreihe von der kleinen Grösse 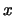 entwickeln, erhalten wir
entwickeln, erhalten wir
Das erste Glied hängt nur von der Zeit ab und kommt bei der Aufstellung der BG nicht vor.
Im zweiten Glied ist
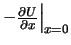 die äussere Kraft,
die auf das System in der Gleichgewichtslage wirkt und eine vorgegebene Funktion der Zeit ist.
Wir bezeichnen sie mit
die äussere Kraft,
die auf das System in der Gleichgewichtslage wirkt und eine vorgegebene Funktion der Zeit ist.
Wir bezeichnen sie mit 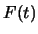 . Damit erscheint in der potentiellen Energie das Glied
. Damit erscheint in der potentiellen Energie das Glied
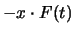 , so dass die Lagrange Funktion des Systems lautet
, so dass die Lagrange Funktion des Systems lautet
Die entsprechende BG ist
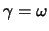
wo wir wiederum die Frequenz 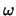 der freien Schwingung eingeführt haben.
Wir betrachten nun einen Fall von besonderem Interesse,
bei dem die äussere Kraft ebenfalls eine einfache periodische Funktion der Zeit mit der
Frequenz
der freien Schwingung eingeführt haben.
Wir betrachten nun einen Fall von besonderem Interesse,
bei dem die äussere Kraft ebenfalls eine einfache periodische Funktion der Zeit mit der
Frequenz 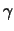 ist:
ist:
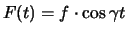 darstellt.
Um eine spezielle Lösung zu suchen, führen wir den Ansatz
darstellt.
Um eine spezielle Lösung zu suchen, führen wir den Ansatz
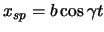 durch,
mit dem gleichen periodischen Faktor. Einsetzen in die DG ergibt
die charakteristische Gleichung
durch,
mit dem gleichen periodischen Faktor. Einsetzen in die DG ergibt
die charakteristische Gleichung
deren Lösung
 ist. Die allgemeine Lösung der inhom. DG ist
ist. Die allgemeine Lösung der inhom. DG ist
Die freien Konstanten 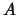 und
und 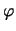 bestimmen sich aus den Anfangsbedingungen.
Das bedeutet, dass das System unter der Wirkung äusserer periodischer Kräfte
eine Bewegung ausführt, die sich aus zwei Schwingungen zusammensetzt. Aus einer
Schwingung mit der Eigenfrequenz
bestimmen sich aus den Anfangsbedingungen.
Das bedeutet, dass das System unter der Wirkung äusserer periodischer Kräfte
eine Bewegung ausführt, die sich aus zwei Schwingungen zusammensetzt. Aus einer
Schwingung mit der Eigenfrequenz 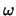 des Systems
und aus einer Schwingung mit der
Frequenz
des Systems
und aus einer Schwingung mit der
Frequenz 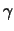 der äusseren Kraft. Der Verlauf der Amplitude der speziellen
Lösung ist in der folgenden Skizze dargestellt:
Die negative Amplitude für
der äusseren Kraft. Der Verlauf der Amplitude der speziellen
Lösung ist in der folgenden Skizze dargestellt:
Die negative Amplitude für
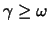 kann man auch als positive Amplitude einer um
kann man auch als positive Amplitude einer um 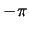 verschobenen
verschobenen
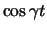 darstellen, d.h. die Lösung lässt sich als
darstellen, d.h. die Lösung lässt sich als
darstellen.
Die gegebene Lösung gilt nicht im Fall der sog. Resonanz, d.h.
wenn die Frequenz der äusseren Kraft mit der Eigenfrequenz des
Systems zusammenfällt. Um die allgemeine Lösung der BG in diesem Falle zu finden, versuchen
wir eine spezielle Lösung mit dem Ansatz
zu finden. Die Motivation für diesen Ansatz ist die folgende: In der vorigen Lösung
strebte der Denominator für
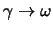 nach Null. Damit diese Divergenz
auf irgendeine Weise kompensiert wird und eine wohldefinierte Lösung existiert, müssen
wir dafür sorgen, dass auch der Numerator für
nach Null. Damit diese Divergenz
auf irgendeine Weise kompensiert wird und eine wohldefinierte Lösung existiert, müssen
wir dafür sorgen, dass auch der Numerator für
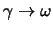 nach
nach 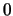 strebt.
Einsetzen in der DG (zuerst nehmen wir formell
strebt.
Einsetzen in der DG (zuerst nehmen wir formell
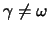 ) ergibt
) ergibt
Die Funktion, die die Lösung im Fall der Resonanz darstellt, finden wir
als Resultat von
Durch Benutzung der triginometrischen Identität
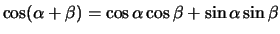 erhalten wir
erhalten wir
und
Die allgemeine Lösung lautet dann
Im Resonanzfall, steigt die Schwingungsamplitude linear mit der Zeit
(solange sie nicht so gross wird, dass die gesamte dargelegte Theorie nicht
mehr anwendbar ist!).
Abbildung 4.1:
Verlauf der Schwingung im Resonanzfall
|
|
Die Erscheinung der Resonanz hat viele Anwendungen in der Physik und überhaupt
in den Naturwissenschaften. Auf einige davon werden wir näher eingehen. Die Resonanz
kann aber auch sehr gefährlich werden, z.B. für Maschinenteile wie Turbinenwellen,
wenn die Eigenfrequenz der Welle gleich ihrer Umlauffrequenz wird. Beim Anfahren von Gasturbinen,
bei denen die Betriebsfrequenz oberhalb der Eigenfrequenz liegt, muss deshalb möglichst
schnell über die Resonanzstelle hinweg gefahren werden.
Neben der Amplitude ist auch die von der äusseren Kraft zugeführte Energie
(oder Arbeit) eine Grösse, die oft den Resonanzprozess charakterisiert.
Die Energie eines Systems, das erzwungene Schwingungen ausführt, bleibt nämlich nicht
erhalten. Diese Tatsache lässt sich direkt aus der in der Lagrange-Funktion vorkommenden
expliziten Zeitabhängigkeit herleiten. Nach unseren Definitionen ist die in einer
Periode
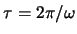 zugeführten Energie
zugeführten Energie
Wir unterscheiden zwischen zwei Fällen:
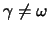 und
und
 .
Im ersten Fall ist die zugefügte Energie (oder, anders ausgedrückt,
die vom System absorbierte Energie) null:
.
Im ersten Fall ist die zugefügte Energie (oder, anders ausgedrückt,
die vom System absorbierte Energie) null:
Nur im Resonanzfall ist das System imstande, Energie zu absorbieren, nämlich
Diese Möglichkeit, nur bei der Resonanz einem System Energie zuzuführen, ist die Grundlage für die Absorption von
Licht durch Materie, und findet zum Beispiel in der Spektroskopie eine wichtige Anwendung ( die 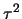 -Abhängigkeit der
absorbierten Energie wird in der Tat nicht beobachtet: Man beobachtet eher eine
-Abhängigkeit der
absorbierten Energie wird in der Tat nicht beobachtet: Man beobachtet eher eine 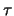 -Abhängigkeit,
die dazu führt, dass die absorbierte Energie pro Zeiteinheit konstant ist. Wir werden sehen, wie die Einführung der
Dämpfung zur nötigen Korrektur führt.)
-Abhängigkeit,
die dazu führt, dass die absorbierte Energie pro Zeiteinheit konstant ist. Wir werden sehen, wie die Einführung der
Dämpfung zur nötigen Korrektur führt.)
Bis jetzt haben wir angenommen, dass die Bewegung der Masse im
leeren Raum stattfindet, oder dass der Einfluss des Mediums auf die Bewegung vernachlässigbar ist.
In Wirklichkeit setzt das Medium der Bewegung des Körpers einen Widerstand entgegen, der
sie zu verlangsamen sucht. Die Energie des sich bewegenden Körpers geht hierbei letzen Endes in
Wärme (oder Strahlung) über - man sagt, sie dissipiert. Der Bewegungsprozess ist unter diesen
Bedingungen schon kein rein mechanischer Vorgang mehr. Beispielweise kann man im Allgemeinen nicht
mehr behaupten, dass die Beschleunigung eines bewegten Körpers nur von seinen Koordinaten
und von der Geschwindigkeit zu einem gegebenen Zeitpunkt abhängt; d.h, BG im Sinne, wie sie
in der Mechanik vorkommen, existieren nicht. Die Bewegung hängt auch von anderen Parametern ab,
zum Beispiel von der Temperatur sowohl des Körpers als auch der des Mediums.
Oft simuliert man solche dissipativen Vorgänge, indem man eine Reibungskraft
in die BG einführt. Eine solche Reibungskraft nimmt für den hier betrachteten Fall der
eindimensionalen Schwingung die Form
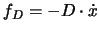 ,
, 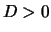 an.
Das Minuszeichen bedeutet, dass die Kraft der Bewegung entgegenwirkt.
Wenn wir diese Kraft auf der rechten Seite der BG hinzufügen, erhalten wir (zuerst sei
an.
Das Minuszeichen bedeutet, dass die Kraft der Bewegung entgegenwirkt.
Wenn wir diese Kraft auf der rechten Seite der BG hinzufügen, erhalten wir (zuerst sei  )
)
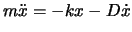 . Wir teilen durch
. Wir teilen durch 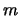 und führen die Bezeichnungen
und führen die Bezeichnungen
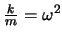 ,
,
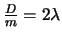 ein. Dabei ist
ein. Dabei ist 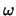 die Frequenz der freien Schwingungen des Systems ohne Reibung.
Die Grösse
die Frequenz der freien Schwingungen des Systems ohne Reibung.
Die Grösse 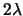 heisst Dämpfungskonstante. Auf diese Weise erhalten wir die Gleichung
heisst Dämpfungskonstante. Auf diese Weise erhalten wir die Gleichung
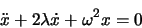
Nach den allgemeinen Regeln für die Lösung linearer DG mit konstanten Koeffizienten
setzen wir den Ansatz
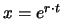 und finden die charakteristische Gleichung
und finden die charakteristische Gleichung
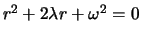 mit den Lösungen
mit den Lösungen
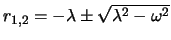 .
Die allgemeine Lösung der Gleichung ist
.
Die allgemeine Lösung der Gleichung ist
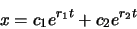
Hier müssen zwei Fälle unterschieden werden:
Für
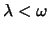 erhalten wir zwei komplex konjugierte Werte für
erhalten wir zwei komplex konjugierte Werte für 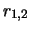 :
:
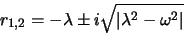
Die allgemeine Lösung der DG ist
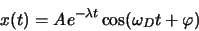
 . Die durch diese Formel dargestellte Bewegung
ist eine sog. gedämpfte Schwingung. Man kann sie als harmonische Schwingung mit exponentiell
abnehmender Amplitude ansehen. Die Schwingungsfrequenz ist kleiner als die Frequenz der freien
Schwingung ohne Reibung.
Wir nehmen jetzt an, dass
. Die durch diese Formel dargestellte Bewegung
ist eine sog. gedämpfte Schwingung. Man kann sie als harmonische Schwingung mit exponentiell
abnehmender Amplitude ansehen. Die Schwingungsfrequenz ist kleiner als die Frequenz der freien
Schwingung ohne Reibung.
Wir nehmen jetzt an, dass
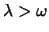 ist. Dann sind beide Werte von
ist. Dann sind beide Werte von 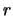 reell und negativ.
Die allgemeine Lösung lautet hier
reell und negativ.
Die allgemeine Lösung lautet hier
Die Bewegung besteht aus einer asymptotischen (bei
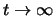 ) Annäherung
an die Gleichgewichtslage ohne Schwingung. Diese Bewegung heisst aperiodisch. Im Automobilbau
ist das die Aufgabe der Stossdämpfer, die durch starke Bodenunebenheiten entstehenden unangenehmen
und auch gefährlichen Federschwingungen der Karrosserie sofern als möglich aperiodisch zu
dämpfen.
) Annäherung
an die Gleichgewichtslage ohne Schwingung. Diese Bewegung heisst aperiodisch. Im Automobilbau
ist das die Aufgabe der Stossdämpfer, die durch starke Bodenunebenheiten entstehenden unangenehmen
und auch gefährlichen Federschwingungen der Karrosserie sofern als möglich aperiodisch zu
dämpfen.
Dissipative Vorgänge spielen natürlich auch bei erzwungenen Schwingungen eine grosse Rolle.
Sie modifizieren den Verlauf des Resonanzvorganges, indem sie auch entfernt von der Resonanz
zur Absorption der Energie führen können. Dabei bremsen sie das Wachstum der Amplitude
im Resonanzfall zu einem endlichen, stationären Wert.
Die DG lautet
Die allgemeine Lösung ist dann (ohne Herleitung)
mit
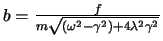 und
und
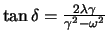 .
Der erste Summand nimmt mit der Zeit exponentiell ab, sodass nach genügend langer Zeit nur
noch der ''erzwungene'' Term
.
Der erste Summand nimmt mit der Zeit exponentiell ab, sodass nach genügend langer Zeit nur
noch der ''erzwungene'' Term
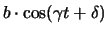 übrigbleibt.
übrigbleibt.
Abbildung 4.2:
Die Phase 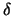 und die Amplitude
und die Amplitude 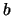 als Funktion von
als Funktion von 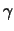 für zwei verschiedene Parameter
für zwei verschiedene Parameter 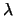
|
|
Die Phase wechselt nicht sprunghaft von 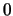 zu
zu 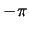 wie beim Fall
wie beim Fall  . Der Wechsel
findet in einem engen Frequenzbereich der Breite
. Der Wechsel
findet in einem engen Frequenzbereich der Breite 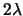 in der Umgebung von
in der Umgebung von 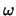 statt.
Am besten schätzen wir die Wirkung der dissipativen Kraft, indem wir die absorbierte Energie
im Fall
statt.
Am besten schätzen wir die Wirkung der dissipativen Kraft, indem wir die absorbierte Energie
im Fall 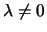 betrachten. Die in einer Periode absorbierte Energie ist
betrachten. Die in einer Periode absorbierte Energie ist
Die entsprechende absorbierte Leistung ist
Abbildung 4.3:
Absorbierte Leistung
|
|
Im eingeschwungenen Zustand bleibt die Energie eines Systems,
das erzwungene Schwingungen ausführt, unverändert. Das System absorbiert allerdings
ununterbrochen Energie (aus der Quelle der äusseren Kraft), die infolge der Reibung dissipiert.
Bei der Resonanzfrequenz ist die aufgenommene Leistung maximal, die
scharfe Resonanzlinie bekommt eine endliche Breite. In der Technik führt man oft zur
Charakterisierung der Schärfe einer Resonanzlinie den sog. Q-Faktor als
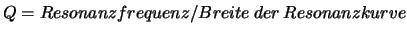 ein.
Da Resonanzerscheinungen eine sehr wichtige Rolle in der Natur spielen und fast auf allen
Gebieten der Physik vorkommen, wollen wir einige davon besprechen.
ein.
Da Resonanzerscheinungen eine sehr wichtige Rolle in der Natur spielen und fast auf allen
Gebieten der Physik vorkommen, wollen wir einige davon besprechen.
Beispiel 1: Elektrische Resonanzkreise
Ein einfacher elektrischer Resonanzkreis (oder Schwingungskreis) besteht
aus einer Serienschaltung einer Kapazität 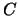 ,
einer Induktivität
,
einer Induktivität 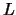 und eines Widerstandes
und eines Widerstandes 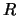 ,
hier abgebildet.
,
hier abgebildet.
Die veränderliche Grösse im elektrischen Schwingkreis ist die transportierte Ladung 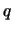 in
Analogie zu
in
Analogie zu 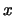 bei der mechanischen harmonischen Schwingung. Die Schwingungsgleichung
für obigen elektrischen Kreis lautet
bei der mechanischen harmonischen Schwingung. Die Schwingungsgleichung
für obigen elektrischen Kreis lautet
Die Halbwertsbreite der Resonanzkurve beträgt in diesem Fall 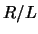 .
Vergleichen wir die beiden Differentialgleichungen für
.
Vergleichen wir die beiden Differentialgleichungen für 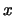 und
und 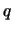 , so können wir eine
rein formale Beziehung entsprechender Grössen finden, die in dieser Tabelle aufgezählt sind.
, so können wir eine
rein formale Beziehung entsprechender Grössen finden, die in dieser Tabelle aufgezählt sind.
|
Charakteristika |
Mech. System |
Elektr. System |
|
Unabhängige Veränderliche |
t |
t |
|
Abhängige Variable |
x |
q |
|
Trägheit |
m |
L |
|
Dämpfung |
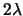 |
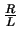 |
|
Resonanzfrequenz (Eigenfreq.) |
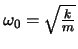 |
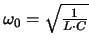 |
|
Schwingungsdauer (Periode) |
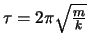 |
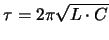 |
|
Q-Faktor |
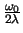 |
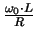 |
Beispiel 2: Spektroskopien
Man kann die Wechselwirkung zwischen einem System mit atomarer Ausdehnung und elektromagnetischer Strahlung
durch eine klassische erzwungene Schwingung simulieren, indem man die von aussen angelegte Störkraft mit dem
elektrischen Feld der Strahlung identifiziert. Systeme mit atomarer Ausdehnung sind durch diskrete Energiewerte
charakterisiert, d.h. dürfen nur bestimmte Energiewerte annehmen. Die ''Eigenfrequenz'' 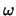 stellt eine
charakteristische Frequenz des Systems dar, und zwar ist sie ein Mass für den Abstand zwischen zwei Eenrgieniveaus,
stellt eine
charakteristische Frequenz des Systems dar, und zwar ist sie ein Mass für den Abstand zwischen zwei Eenrgieniveaus,
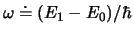 , wobei
, wobei
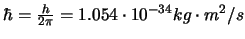 das Plank'sche Wirkungsquantum ist. Dieses Modell führt zum Phänomen, dass nur bei
der Resonanzfrequenz das System vom elektromagnetischen Energiefeld absorbieren kann.
Diese Absorption erfolgt durch den Übergang des Systems vom niedrigen Energieniveau
das Plank'sche Wirkungsquantum ist. Dieses Modell führt zum Phänomen, dass nur bei
der Resonanzfrequenz das System vom elektromagnetischen Energiefeld absorbieren kann.
Diese Absorption erfolgt durch den Übergang des Systems vom niedrigen Energieniveau 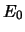 zum angeregten Zustand
zum angeregten Zustand  . Durch diese Resonanzerscheinung entsteht die Möglichkeit, die
Energieniveaus eines Systems zu bestimmen: das ist die Grundlage der Spektroskopie, da es ermöglicht,
verschiedene Systeme anhand deren Absorpsionsspektren zu erkennen.
Mögliche angeregte Zustände eines Moleküls sind Schwingungen, für welche
. Durch diese Resonanzerscheinung entsteht die Möglichkeit, die
Energieniveaus eines Systems zu bestimmen: das ist die Grundlage der Spektroskopie, da es ermöglicht,
verschiedene Systeme anhand deren Absorpsionsspektren zu erkennen.
Mögliche angeregte Zustände eines Moleküls sind Schwingungen, für welche 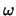 mit der
klassischen Schwingungsfrequenz übereinstimmt. Schwingungen führen zur Absorption im Infrarotbereich:
man sprich von Infrarotspektroskopie.
Ein typisches Absorptionsspektrum verursacht durch Schwingungen, ist in der Figur aufgezeichnet.
mit der
klassischen Schwingungsfrequenz übereinstimmt. Schwingungen führen zur Absorption im Infrarotbereich:
man sprich von Infrarotspektroskopie.
Ein typisches Absorptionsspektrum verursacht durch Schwingungen, ist in der Figur aufgezeichnet.
Die transmittierte Lichtintensität als Funktion der Wellenlänge des einfallendes Lichts zeigt ein deutliches
Transmissionsminimum, entsprechend einer Energieaufnahme der Moleküle, also einer Anregung von
Schwingungen. Solche Minima sind charakteristisch für die betreffende Substanz, und der Chemiker
kann daraus die Natur und Art der zu untersuchenden Probe bestimmen.
Absorption im Ultravioletten deutet auf elektronische Anregungen hin, wie der übergang zwischen zwei
Energieniveaus im Wasserstoffatom.
Die ''Natriumflamme'' ist ein typisches Beispiel einer elektronischen Anregung. Das
Na-Atom besitzt in seiner elektonischen Struktur zwei benachbarte Niveaus, deren Abstand gelbem
Licht entspricht. Auf ein Drahtnetz, das in der Flamme
eines Bunsenbrenners steht, wird Kochsalz gestreut, und die Flamme leuchtet gelb, entsprechend der
Wellenlänge des gelben Na-Lichtes 5890 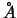 . Durch das Erhitzen werden einige Atome in einen angeregten
Zustand versetzt.
Die angeregten Atome bleiben jedoch
nur sehr kurze Zeit
. Durch das Erhitzen werden einige Atome in einen angeregten
Zustand versetzt.
Die angeregten Atome bleiben jedoch
nur sehr kurze Zeit
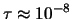 sec in diesem angeregten Zustand und
fallen wieder auf ihr Ausgangsniveau zurück. Dabei emittieren sie Licht mit der charakteristischen Na-Wellenlänge.
Beleuchten wir die Flamme mit
einer Natrium-Spektrallampe, die genau diese Wellenlänge emittiert, so beobachten wir an der
bestrahlten Stelle der Flamme auf einem dahinter aufgestellten Schirm schwarze Zonen.
Durch das Einstrahlen der Resonanzfrequenz
sec in diesem angeregten Zustand und
fallen wieder auf ihr Ausgangsniveau zurück. Dabei emittieren sie Licht mit der charakteristischen Na-Wellenlänge.
Beleuchten wir die Flamme mit
einer Natrium-Spektrallampe, die genau diese Wellenlänge emittiert, so beobachten wir an der
bestrahlten Stelle der Flamme auf einem dahinter aufgestellten Schirm schwarze Zonen.
Durch das Einstrahlen der Resonanzfrequenz 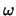 werden die Atome energetisch in den angeregten
Zustand versetzt. Ein Teil des einfallenden Lichts wird für diesen Prozess benutzt, und verschwindet.
Das durch spontane Emission reemittierte Licht
geht in jeden Raumwinkel
und fehlt daher zu einem hohen Prozentsatz in der Durchstrahlrichtung: ein Schatten ensteht. Aufgrund der
endlichen Lebensdauer, besitzen die Niveaus eine gewisse Breite
werden die Atome energetisch in den angeregten
Zustand versetzt. Ein Teil des einfallenden Lichts wird für diesen Prozess benutzt, und verschwindet.
Das durch spontane Emission reemittierte Licht
geht in jeden Raumwinkel
und fehlt daher zu einem hohen Prozentsatz in der Durchstrahlrichtung: ein Schatten ensteht. Aufgrund der
endlichen Lebensdauer, besitzen die Niveaus eine gewisse Breite
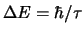 : auch benachbarte
Frequenzen können am Resonanzprozess teilnehmen.
In der Tabelle sind die charakteristischen Absorptionsbereiche, mit den entsprechenden Anregungen,
zusammengefasst.
: auch benachbarte
Frequenzen können am Resonanzprozess teilnehmen.
In der Tabelle sind die charakteristischen Absorptionsbereiche, mit den entsprechenden Anregungen,
zusammengefasst.
|
Spektralgebiet |
Art der Anregung |
|
Ultra-violett (UV) |
Schwingungen der Valenzelektronen |
|
Infrarot (IR) |
Molekülvibrationen |
|
Mikrowellen |
Molekülrotationen |
Die Absorptionsmaxima im UV einiger typischer organischer
Substanzen mit Mehrfachbindungen sind im Folgenden aufgezählt.
|
Verbindung |
Wellenlänge des Absorptionsmaximums |
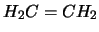 |
1625Å |
 |
1775Å |
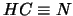 |
1750Å |
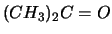 |
1870Å |
Resonanzphänomene beobachtet man auch in der Kernspektroskopie.
Dabei tritt eine besondere Schwierigkeit auf: bei der Emission eines
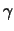 -Quants erfährt der Kern aus Impulserhaltungsgründen einen Rückstoss. Einen Rückstoss erfahren auch Atome,
dieser ist allerdings vernachlässigbar klein. Durch diesen Rückstoss besitzt das emittierte
Quant eine um die Rückstossenergie verringerte Energie. Da der Impuls eines Quants
-Quants erfährt der Kern aus Impulserhaltungsgründen einen Rückstoss. Einen Rückstoss erfahren auch Atome,
dieser ist allerdings vernachlässigbar klein. Durch diesen Rückstoss besitzt das emittierte
Quant eine um die Rückstossenergie verringerte Energie. Da der Impuls eines Quants 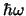 :
:
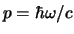 ist,
muss der gleiche
Impuls vom Kern als Rückstoss aufgenommen werden. Die Rückstossenergie eines Kerns der Masse
ist,
muss der gleiche
Impuls vom Kern als Rückstoss aufgenommen werden. Die Rückstossenergie eines Kerns der Masse
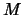 beträgt deshalb:
beträgt deshalb:
Abbildung 4.4:
Energieschema beim Mössbauereffekt (rechts)
|
|
Betrachten wir zwei benachbarte Kernzustände, deren Energiedifferenz 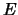 gegeben sei.
Bei der Emission eines
gegeben sei.
Bei der Emission eines 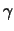 -Quants geht der Kern vom Zustand II in den Zustand I über.
Die Energie des
-Quants geht der Kern vom Zustand II in den Zustand I über.
Die Energie des 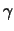 -Quants ist gleich der Energiedifferenz der beiden Zustände
-Quants ist gleich der Energiedifferenz der beiden Zustände 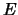 ,
vermindert um die Rückstossenergie
,
vermindert um die Rückstossenergie 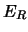 , also
, also
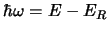 . Da die Kernniveaus ausserordentlich scharf sind,
viel schärfer als atomare Niveaus, reicht diese
. Da die Kernniveaus ausserordentlich scharf sind,
viel schärfer als atomare Niveaus, reicht diese 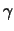 -Energie
-Energie 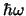 nicht mehr aus, um einen anderen Kern
vom Niveau I
auf das Niveau II anzuregen; oder mit anderen Worten: man kann einen Kern nicht als Photonenquelle für die Spektroskopie
anderer ähnlicher Kerne benutzen.
nicht mehr aus, um einen anderen Kern
vom Niveau I
auf das Niveau II anzuregen; oder mit anderen Worten: man kann einen Kern nicht als Photonenquelle für die Spektroskopie
anderer ähnlicher Kerne benutzen.
Dieses Bild ist nicht ganz korrekt: der Münchner Physiker Rudolf Mössbauer fand einen beträchtlichen Teil an
resonanter Absorption bei Kernen
(für diese Entdeckung erhielt er 1961 den Nobelpreis). Dieser Effekt wurde von Mössbauer folgendermassen erklärt.
Betrachten wir die Gleichung für 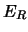 , so erkennen wir
die Abhängigkeit der Rückstossenergie
, so erkennen wir
die Abhängigkeit der Rückstossenergie 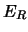 von der Masse des Kerns
von der Masse des Kerns 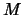 , der
den Rückstoss aufnimmt. Sind die
, der
den Rückstoss aufnimmt. Sind die 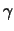 -emittierenden Kerne sowie die absorbierenden
Kerne in ein Kristallgitter eingebaut, so wird der Rückstoss bei Emission nicht von einem
einzelnen Kern der Masse
-emittierenden Kerne sowie die absorbierenden
Kerne in ein Kristallgitter eingebaut, so wird der Rückstoss bei Emission nicht von einem
einzelnen Kern der Masse 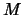 , sondern mit einer bestimmten Wahrscheinlichkeit von dem umgebenden
Kristallgitter als ganzes aufgenommen. In der Gleichung für
, sondern mit einer bestimmten Wahrscheinlichkeit von dem umgebenden
Kristallgitter als ganzes aufgenommen. In der Gleichung für
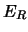 müssen wir daher in bestimmten Fällen die Masse
müssen wir daher in bestimmten Fällen die Masse 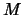 durch eine sehr grosse Masse
ersetzen, dabei wird die Rückstossenergie
durch eine sehr grosse Masse
ersetzen, dabei wird die Rückstossenergie 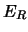 beliebig klein, d.h. die Energie
des
beliebig klein, d.h. die Energie
des 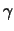 -Quants wird wieder gleich der Differenz der Kenergiezustände. Diese
-Quants wird wieder gleich der Differenz der Kenergiezustände. Diese
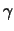 -Strahlung kann von einem anderen Kern resonant absorbiert werden.
Eines der Isotope, das heutzutage am häufigsten für Mössbauereffektmessungen verwendet
wird, ist
-Strahlung kann von einem anderen Kern resonant absorbiert werden.
Eines der Isotope, das heutzutage am häufigsten für Mössbauereffektmessungen verwendet
wird, ist 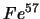 mit der 14,4 keV
mit der 14,4 keV 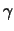 -Linie. Die Linienbreite ist von der Grössenordnung
-Linie. Die Linienbreite ist von der Grössenordnung
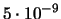 eV. Damit wird der Q-Faktor von der Grössenordnung
eV. Damit wird der Q-Faktor von der Grössenordnung 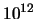 .
Darin liegt die grosse Bedeutung des Mössbauereffektes. Man hat ein äusserst
empfindliches Werkzeug zur Hand, um z.B. relativistische Effekte, Magnetfelder,
Verschiebungen im Kristallgitter usw. zu messen.
.
Darin liegt die grosse Bedeutung des Mössbauereffektes. Man hat ein äusserst
empfindliches Werkzeug zur Hand, um z.B. relativistische Effekte, Magnetfelder,
Verschiebungen im Kristallgitter usw. zu messen.
Mössbauer selbst hat diesen Effekt der rückstossfreien Kern-Resonanzabsorption zuerst an
Iridium 191 gefunden (Z. f. Physik 151, 124, 1958). Es sind heutzutage mehr als 80
Isotope bekannt, die für den Mössbauereffekt geeignet sind. Stichwortartig seien in folgender
Tabelle einige Beispiele von Anwendungen des Mössbauereffektes aufgezählt.
Die wohl grösste Bedeutung hat der Mössbauereffekt für die Aufklärung der
Strukturen fester Körper.
|
Gebiet |
Anwendung |
|
Relativität |
Frequenzverschiebung eines Lichtquants |
|
|
im Gravitationsfeld |
|
Kernphysik |
Bestimmung magnetischer Momente von |
|
|
angeregten Zuständen |
|
Kernphysik |
Quadrupoleffekte |
|
Kernphysik |
Bestimmung von Kernradien |
|
Festkörperphysik |
Elektrischer Feldgradient am Kernort |
|
Festkörperphysik |
Messung von inneren Magnetfeldern in Kristallen |
|
Festkörperphysik |
Magnetische Kristallstruktur |
|
Festkörperphysik |
Strahlungsschäden |
|
Chemie |
Isomerieveschiebung |
|
Chemie |
Hüllenordnungen nach Kernprozessen |
|
Chemie |
Strukturaufklärung komplizierter Moleküle |
Wir schliessen mit der Illustration von Resonanzen in der Teilchenphysik. Schiesst man z.B. Neutronen auf Iridiumkerne
oder 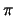 -Mesonen auf Protonen,
so können für sehr kurze Zeiten sog. Resonanzen entstehen, kurzlebige Kombinationsteilchen,
die kurz nach ihrer Bildung zerfallen. Das Auftreten einer Resonanz äussert sich in der
Abhängigkeit der Wahrscheinlichkeit
-Mesonen auf Protonen,
so können für sehr kurze Zeiten sog. Resonanzen entstehen, kurzlebige Kombinationsteilchen,
die kurz nach ihrer Bildung zerfallen. Das Auftreten einer Resonanz äussert sich in der
Abhängigkeit der Wahrscheinlichkeit 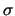 für eine bestimmte Reaktion von der Energie:
Aus der Breite der Resonanzabsorption, welche gleich
für eine bestimmte Reaktion von der Energie:
Aus der Breite der Resonanzabsorption, welche gleich 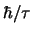 ist, liest man die
Lebensdauer
ist, liest man die
Lebensdauer 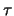 des Kombinationsteilchens ab. Das zeigt, dass Resonanzen auch in der
Kern-und Teilchenphysik von Bedeutung sind: neue Teilchen zeigen sich oft nur als Resonanz in einem Streuexperiment.
des Kombinationsteilchens ab. Das zeigt, dass Resonanzen auch in der
Kern-und Teilchenphysik von Bedeutung sind: neue Teilchen zeigen sich oft nur als Resonanz in einem Streuexperiment.




Nächste Seite: Die lineare schwingende Kette
Aufwärts: Schwingungen
Vorherige Seite: Eindimensionale harmonische Schwingung
Inhalt
Kraeutler Vincent
2000-05-30
![\includegraphics [width=5cm]{f41.eps}](img572.png)
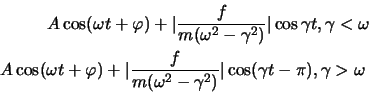
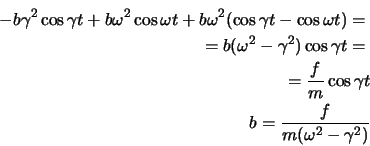
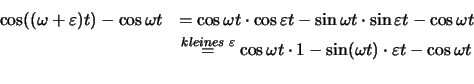
![]() zugeführten Energie
zugeführten Energie

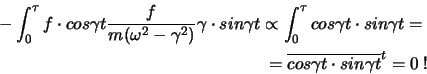
![]() ,
, ![]() an.
Das Minuszeichen bedeutet, dass die Kraft der Bewegung entgegenwirkt.
Wenn wir diese Kraft auf der rechten Seite der BG hinzufügen, erhalten wir (zuerst sei
an.
Das Minuszeichen bedeutet, dass die Kraft der Bewegung entgegenwirkt.
Wenn wir diese Kraft auf der rechten Seite der BG hinzufügen, erhalten wir (zuerst sei ![]() )
)
![]() . Wir teilen durch
. Wir teilen durch ![]() und führen die Bezeichnungen
und führen die Bezeichnungen
![]() ,
,
![]() ein. Dabei ist
ein. Dabei ist ![]() die Frequenz der freien Schwingungen des Systems ohne Reibung.
Die Grösse
die Frequenz der freien Schwingungen des Systems ohne Reibung.
Die Grösse ![]() heisst Dämpfungskonstante. Auf diese Weise erhalten wir die Gleichung
heisst Dämpfungskonstante. Auf diese Weise erhalten wir die Gleichung
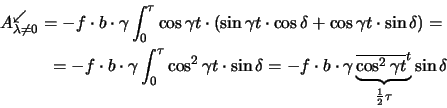
![]() ,
einer Induktivität
,
einer Induktivität ![]() und eines Widerstandes
und eines Widerstandes ![]() ,
hier abgebildet.
,
hier abgebildet.
![\includegraphics [width=5cm]{f46.eps}](img630.png)
![]() stellt eine
charakteristische Frequenz des Systems dar, und zwar ist sie ein Mass für den Abstand zwischen zwei Eenrgieniveaus,
stellt eine
charakteristische Frequenz des Systems dar, und zwar ist sie ein Mass für den Abstand zwischen zwei Eenrgieniveaus,
![]() , wobei
, wobei
![]() das Plank'sche Wirkungsquantum ist. Dieses Modell führt zum Phänomen, dass nur bei
der Resonanzfrequenz das System vom elektromagnetischen Energiefeld absorbieren kann.
Diese Absorption erfolgt durch den Übergang des Systems vom niedrigen Energieniveau
das Plank'sche Wirkungsquantum ist. Dieses Modell führt zum Phänomen, dass nur bei
der Resonanzfrequenz das System vom elektromagnetischen Energiefeld absorbieren kann.
Diese Absorption erfolgt durch den Übergang des Systems vom niedrigen Energieniveau ![]() zum angeregten Zustand
zum angeregten Zustand ![]() . Durch diese Resonanzerscheinung entsteht die Möglichkeit, die
Energieniveaus eines Systems zu bestimmen: das ist die Grundlage der Spektroskopie, da es ermöglicht,
verschiedene Systeme anhand deren Absorpsionsspektren zu erkennen.
Mögliche angeregte Zustände eines Moleküls sind Schwingungen, für welche
. Durch diese Resonanzerscheinung entsteht die Möglichkeit, die
Energieniveaus eines Systems zu bestimmen: das ist die Grundlage der Spektroskopie, da es ermöglicht,
verschiedene Systeme anhand deren Absorpsionsspektren zu erkennen.
Mögliche angeregte Zustände eines Moleküls sind Schwingungen, für welche ![]() mit der
klassischen Schwingungsfrequenz übereinstimmt. Schwingungen führen zur Absorption im Infrarotbereich:
man sprich von Infrarotspektroskopie.
Ein typisches Absorptionsspektrum verursacht durch Schwingungen, ist in der Figur aufgezeichnet.
mit der
klassischen Schwingungsfrequenz übereinstimmt. Schwingungen führen zur Absorption im Infrarotbereich:
man sprich von Infrarotspektroskopie.
Ein typisches Absorptionsspektrum verursacht durch Schwingungen, ist in der Figur aufgezeichnet.
![\includegraphics [width=12cm]{f47.eps}](img645.png)
![\includegraphics [width=12cm]{f48.eps}](img648.png)
![]() -Quants erfährt der Kern aus Impulserhaltungsgründen einen Rückstoss. Einen Rückstoss erfahren auch Atome,
dieser ist allerdings vernachlässigbar klein. Durch diesen Rückstoss besitzt das emittierte
Quant eine um die Rückstossenergie verringerte Energie. Da der Impuls eines Quants
-Quants erfährt der Kern aus Impulserhaltungsgründen einen Rückstoss. Einen Rückstoss erfahren auch Atome,
dieser ist allerdings vernachlässigbar klein. Durch diesen Rückstoss besitzt das emittierte
Quant eine um die Rückstossenergie verringerte Energie. Da der Impuls eines Quants ![]() :
:
![]() ist,
muss der gleiche
Impuls vom Kern als Rückstoss aufgenommen werden. Die Rückstossenergie eines Kerns der Masse
ist,
muss der gleiche
Impuls vom Kern als Rückstoss aufgenommen werden. Die Rückstossenergie eines Kerns der Masse
![]() beträgt deshalb:
beträgt deshalb:
![\includegraphics [angle=-2,width=12cm]{f411.eps}](img661.png)
![\includegraphics [angle=-2,width=12cm]{f412.eps}](img665.png)
![\includegraphics [width=12cm]{f413.eps}](img666.png)