



Nächste Seite: Erzwungene Schwingung
Aufwärts: Schwingungen
Vorherige Seite: Schwingungen
Inhalt
Obwohl wir die wesentlichen Merkmale der harmonischen eindimensionalen Schwingung um die Ruhelage schon
physikalisch untersucht haben, wollen wir diese als Ausgangspunkt zu einer systematischen Untersuchung komplizierterer
Arten von Schwingungen zusammenfassen. Wir bezeichnen die eindimensionale Koordinate als 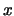 , die eine Schwingung durchläuft.
Lösung von linearen Differentialgleichungen zweiter Ordnung.
In einer linearen DG 2. Ordnung kommen
, die eine Schwingung durchläuft.
Lösung von linearen Differentialgleichungen zweiter Ordnung.
In einer linearen DG 2. Ordnung kommen 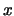 ,
,
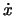 ,
, 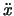 linear vor:
linear vor:
wobei 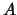 ,
, 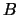 ,
, 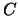 ,
, 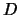 Funktionen von
Funktionen von 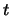 sein
können. Wenn der Term
sein
können. Wenn der Term 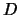 fehlt, nennen wir die
Gleichung homogen. Die allgemeine Lösung der hom. DG ist die lineare Kombination zweier
linear unhabhängiger Lösungen:
fehlt, nennen wir die
Gleichung homogen. Die allgemeine Lösung der hom. DG ist die lineare Kombination zweier
linear unhabhängiger Lösungen:
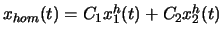 .
Wenn man eine spezielle Lösung
.
Wenn man eine spezielle Lösung 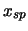 einer inhomogenen
linearen Differentialgleichung gefunden hat, erhält man die allgemeine Lösung der inhom. DG durch
einer inhomogenen
linearen Differentialgleichung gefunden hat, erhält man die allgemeine Lösung der inhom. DG durch
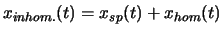 .
Beispiel: Homogene lineare Gleichungen mit konstanten
Koeffizienten
.
Beispiel: Homogene lineare Gleichungen mit konstanten
Koeffizienten 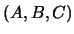 . Solche DG löst man mit dem Ansatz
. Solche DG löst man mit dem Ansatz
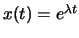 .
Aus der homogenen Differentialgleichung erhält man, durch Einsetzen, die algebraische Gleichung für
.
Aus der homogenen Differentialgleichung erhält man, durch Einsetzen, die algebraische Gleichung für 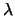 ,
,
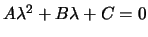 .
Sie wird charakteristische Gleichung genannt.
Ihre zwei Lösungen geben, wenn sie nicht gerade
zusammenfallen, zwei Lösungen der
Differentialgleichung und damit die allgemeine Lösung
.
Sie wird charakteristische Gleichung genannt.
Ihre zwei Lösungen geben, wenn sie nicht gerade
zusammenfallen, zwei Lösungen der
Differentialgleichung und damit die allgemeine Lösung
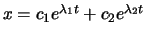 .
.
Wir wollen jetzt diese Betrachtungen für die formale Lösung der Gleichung
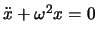 anwenden. Diese Gleichung ist die
zur Lagrange Funktion
anwenden. Diese Gleichung ist die
zur Lagrange Funktion
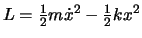 gehörige Lagrange Gleichung, mit
gehörige Lagrange Gleichung, mit
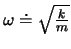 . Die dazugehörige charakteristische Gleichung ist
. Die dazugehörige charakteristische Gleichung ist
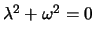 , so dass die allgemeine Lösung ist
, so dass die allgemeine Lösung ist
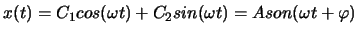 , mit
, mit
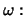 Kreisfrequenz
Kreisfrequenz
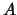 : maximale Amplitude
: maximale Amplitude
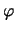 : Phasenwinkel
: Phasenwinkel
-
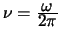 : Frequenz
: Frequenz
-
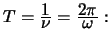 Schwingungsdauer
Schwingungsdauer
Einige Spezialfälle verdienen besondere Beachtung.
- Wir lenken den Oszillator anfangs um
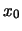 aus, lassen ihn dann los und
betrachten seine Schwingung. Die Anfangsbedingungen lauten offenbar
aus, lassen ihn dann los und
betrachten seine Schwingung. Die Anfangsbedingungen lauten offenbar
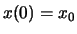 ,
, 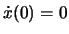 .
Die Lösung zu diesen Anfangsbedingungen ist deshalb
.
Die Lösung zu diesen Anfangsbedingungen ist deshalb
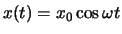 .
Die Anfangselongation ist gleichzeitig die maximal Amplitude der Schwingung.
.
Die Anfangselongation ist gleichzeitig die maximal Amplitude der Schwingung.
- Wir stossen den Körper in seiner Ruhelage an und verleihen ihm die
Geschwindigkeit
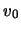 ,
, 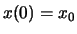 ,
, 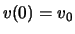 . Dies führt zu
. Dies führt zu
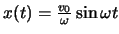 .
Die maximale Amplitude der Schwingung ist somit
.
Die maximale Amplitude der Schwingung ist somit
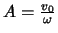 .
.




Nächste Seite: Erzwungene Schwingung
Aufwärts: Schwingungen
Vorherige Seite: Schwingungen
Inhalt
Kraeutler Vincent
2000-05-30
![]() anwenden. Diese Gleichung ist die
zur Lagrange Funktion
anwenden. Diese Gleichung ist die
zur Lagrange Funktion
![]() gehörige Lagrange Gleichung, mit
gehörige Lagrange Gleichung, mit
![]() . Die dazugehörige charakteristische Gleichung ist
. Die dazugehörige charakteristische Gleichung ist
![]() , so dass die allgemeine Lösung ist
, so dass die allgemeine Lösung ist
![]() , mit
, mit