



Nächste Seite: Das Zweikörper-Problem
Aufwärts: Anwendungen der BG
Vorherige Seite: Anwendungen der BG
Inhalt
Die Bewegung eines Massenpunktes mit einem Freiheitsgrad heisst eindimensionale Bewegung. Die Lagrange Funktion einer solchen Bewegung ist
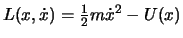 , die dazugehörige BG ist
, die dazugehörige BG ist
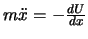 . Diese Gleichung lässt sich folgendermassen integrieren:
. Diese Gleichung lässt sich folgendermassen integrieren:
Die so gewonnene Integrationskonstante 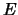 ist ein Integral der Bewegung, da sie mit der Zeit unverändert bleibt.
Diese Konstante heisst totale Energie der Bewegung. Sie kann dazu benutzt werden, um die Bewegungen zu klassifizieren.
Die resultierende DG erster Ordnung lässt sich durch Trennung der Veränderlichen integrieren:
ist ein Integral der Bewegung, da sie mit der Zeit unverändert bleibt.
Diese Konstante heisst totale Energie der Bewegung. Sie kann dazu benutzt werden, um die Bewegungen zu klassifizieren.
Die resultierende DG erster Ordnung lässt sich durch Trennung der Veränderlichen integrieren:
Etwas Allgemeines lernen wir aus dieser Lösung: eine reelle (und somit physikalische) Lösung existiert nur im Gebiet, wo 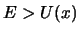 ist.
Diese Gebiete kann man direkt ablesen, wenn man die potentielle Energie graphisch darstellt.
ist.
Diese Gebiete kann man direkt ablesen, wenn man die potentielle Energie graphisch darstellt.
Abbildung 2.1:
Graphische Darstellung von 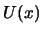
|
|
Die Punkte, bei denen 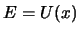 ist, sind Umkehrpunkte der Bahn, da in ihnen die Geschwindigkeit
ist, sind Umkehrpunkte der Bahn, da in ihnen die Geschwindigkeit  wird, und sich somit das Vorzeichen ändern kann.
Man unterscheidet zwischen endlichen Bahnen, die in einem endlichen Raumgebiet verlaufen können, und unendlichen Bahnen,
wenn die Masse ins Unendliche laufen kann. Die eindimensionalen endlichen Bahnen sind Schwingungen: die Masse bewegt sich
zwischen den Umkehrpunkten
wird, und sich somit das Vorzeichen ändern kann.
Man unterscheidet zwischen endlichen Bahnen, die in einem endlichen Raumgebiet verlaufen können, und unendlichen Bahnen,
wenn die Masse ins Unendliche laufen kann. Die eindimensionalen endlichen Bahnen sind Schwingungen: die Masse bewegt sich
zwischen den Umkehrpunkten 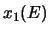 und
und 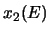 periodisch, d.h. sie kehrt nach einer gewissen Zeit wieder zurück an
einen bestimmten Punkt. Die Periode der Schwingung ist durch den Ausdruck
periodisch, d.h. sie kehrt nach einer gewissen Zeit wieder zurück an
einen bestimmten Punkt. Die Periode der Schwingung ist durch den Ausdruck
gegeben.
Beispiel.
Abbildung 2.2:
verlauf der potentiellen Energie bei der chemische Bindung
|
|
Nach unserer Vorstellung der chemischen Bindung, die zu einem Molekül führt, hat die potentielle Energie zwischen zwei
Atomen folgende Abhängigkeit vom Abstand 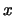 zwischen den Atomen, siehe Abb.2.2.
Aber auch zwischen zwei Atomen in einem Festkörper herrscht ein Potential, das einen ähnlichen Verlauf hat.
Dieser Verlauf führt zur chemischen Bindung beim Gleichgewichtsabstand
zwischen den Atomen, siehe Abb.2.2.
Aber auch zwischen zwei Atomen in einem Festkörper herrscht ein Potential, das einen ähnlichen Verlauf hat.
Dieser Verlauf führt zur chemischen Bindung beim Gleichgewichtsabstand 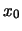 , bei dem U(x) ein Minimum hat.
Dabei ist die Bindungsenergie
, bei dem U(x) ein Minimum hat.
Dabei ist die Bindungsenergie
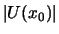 . Warum bei
. Warum bei 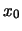 die zwei Atome ''gebunden'' sind, kann man leicht erklären:
sollte ein Atom versuchen, die Gleichgewichtslage zu verlassen, spürt es eine rücktreibende Kraft
die zwei Atome ''gebunden'' sind, kann man leicht erklären:
sollte ein Atom versuchen, die Gleichgewichtslage zu verlassen, spürt es eine rücktreibende Kraft
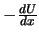 ,
die es wieder zu
,
die es wieder zu 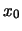 führt. Wenn
führt. Wenn 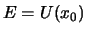 ist, ist das Molekül im Grundzustand. Angeregte Zustände, bei denen
ist, ist das Molekül im Grundzustand. Angeregte Zustände, bei denen
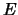 knapp oberhalb des Grundzustandswertes liegt, sind, wie wir gesagt haben, Schwingungen. Wir wollen jetzt die Periode
solcher Schwingungen abschätzen. In der Nähe eines Minimums, lässt sich
knapp oberhalb des Grundzustandswertes liegt, sind, wie wir gesagt haben, Schwingungen. Wir wollen jetzt die Periode
solcher Schwingungen abschätzen. In der Nähe eines Minimums, lässt sich 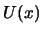 folgenderweise approximieren:
folgenderweise approximieren:
Da 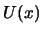 bei
bei 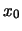 ein Minimum besitzt, ist
ein Minimum besitzt, ist 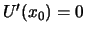 . Das erste nicht verschwindende
Glied ist das proportional zu
. Das erste nicht verschwindende
Glied ist das proportional zu 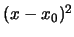 . Damit ist
. Damit ist
Diese Näherung, die nur für kleine Schwingungen gilt, heisst harmonische Approximation. In dieser Näherung
folgt 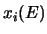 aus der Gleichung
aus der Gleichung
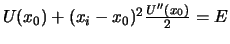 , d.h.
, d.h.
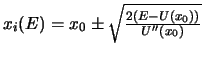 .
Eingesetzt in den Ausdruck für
.
Eingesetzt in den Ausdruck für  ergibt dies
ergibt dies
Das Bemerkenswerte an diesem Resultat ist, dass 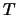 von
von 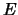 unabängig ist. Dies ist aber nur in der harmonischen Näherung
gültig. Für die Schwingung definiert man eine Schwingungsfrequenz als
unabängig ist. Dies ist aber nur in der harmonischen Näherung
gültig. Für die Schwingung definiert man eine Schwingungsfrequenz als
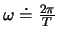 . In der
harmonischen Näherung ist
. In der
harmonischen Näherung ist
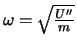 . Die Frequenz ist das fundamentale Charakteristikum
von Schwingungen; sie hängt nicht
von den Anfangsbedingungen der Bewegung ab, sondern ist vollständig durch die mechanische
Eigenschaft des Systems bestimmt. Im Wesentlichen gibt sie
Auskunft über die Krümmung (zweite Ableitung!) der potentiellen Energie in der Nähe der Ruhelage.
Dieses Resultat ist von entscheidender Bedeutung für die Spektroskopie von Molekülen und Festkörpern:
durch die spektroskopische Bestimmung der Schwingungsfrequenz lässt sich etwas über die potentielle Energie der Moleküle aussagen!!
In der harmonischen Näherung, lässt sich die Lösung der BG in einer geschlossenen algebraischen Form schreiben:
. Die Frequenz ist das fundamentale Charakteristikum
von Schwingungen; sie hängt nicht
von den Anfangsbedingungen der Bewegung ab, sondern ist vollständig durch die mechanische
Eigenschaft des Systems bestimmt. Im Wesentlichen gibt sie
Auskunft über die Krümmung (zweite Ableitung!) der potentiellen Energie in der Nähe der Ruhelage.
Dieses Resultat ist von entscheidender Bedeutung für die Spektroskopie von Molekülen und Festkörpern:
durch die spektroskopische Bestimmung der Schwingungsfrequenz lässt sich etwas über die potentielle Energie der Moleküle aussagen!!
In der harmonischen Näherung, lässt sich die Lösung der BG in einer geschlossenen algebraischen Form schreiben:
oder
Der Koeffizient
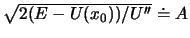 ist die maximale Amplitude der Schwingung um den
Gleichgewichtsabstand,
ist die maximale Amplitude der Schwingung um den
Gleichgewichtsabstand, 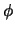 ist die Anfangsphase der Schwingung. Zwischen
ist die Anfangsphase der Schwingung. Zwischen 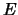 und
und 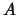 ist
die Beziehung
ist
die Beziehung
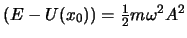 .
Die Energiekonstanz bedeutet, dass beim Durchgang durch die Gleichgewichtslage die totale
Energiezunahme
.
Die Energiekonstanz bedeutet, dass beim Durchgang durch die Gleichgewichtslage die totale
Energiezunahme 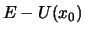 als reine kinetische Energie
im System steckt. In den Umkehrpunkten besteht nur potentielle Energie. Kinetische und potentielle
Energien gehen dauernd ineinander über, wobei die Summe konstant bleibt.
als reine kinetische Energie
im System steckt. In den Umkehrpunkten besteht nur potentielle Energie. Kinetische und potentielle
Energien gehen dauernd ineinander über, wobei die Summe konstant bleibt.
Abbildung 2.3:
Kin. und pot. Energie bei der harmonischen Schwingung
|
|




Nächste Seite: Das Zweikörper-Problem
Aufwärts: Anwendungen der BG
Vorherige Seite: Anwendungen der BG
Inhalt
Kraeutler Vincent
2000-05-30
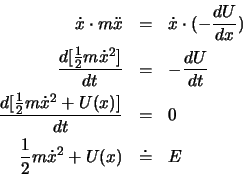
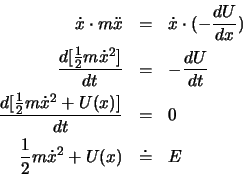
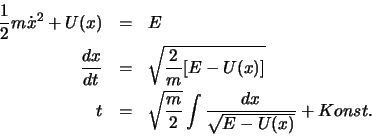
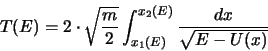
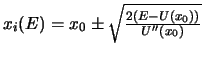 .
Eingesetzt in den Ausdruck für
.
Eingesetzt in den Ausdruck für ![\begin{eqnarray*}
T(E) & = & 2\cdot \sqrt{\frac{m}{2}}\int_{x_1(E)}^{x_2(E)} \f...
...[arcsin(1)-arcsin(-1)]\\
& = & 2\pi \sqrt{\frac{m}{U''(x_0)}}
\end{eqnarray*}](img354.png)
![\begin{eqnarray*}
\omega t & = & \int \frac{dy}{\sqrt{2(E-U(x_0))/U''-y^2}} + Konst\\
& = & arcsin[\frac{y}{\sqrt{2(E-U(x_0))/U''}}] + Konst.
\end{eqnarray*}](img358.png)