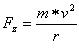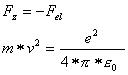|
Bohrsches Atommodell
|
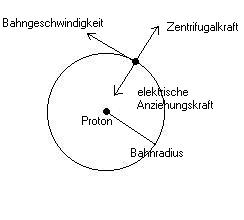
Im Jahre 1913 entwickelte Niels Bohr ein Atommodell für das Wasserstoffatom. Danach umkreist
das 
Elektron das Proton mit einer Geschwindigkeit v. Dabei erfährt es eine Zentrifugalkraft
und eine entgegengesetzt gleich grosse elektrische Anziehungskraft.
Zwischen zwei elektrisch geladenen Teilchen treten elektrostatische Kräfte auf. Zwei gleich
geladene Teilchen stossen sich ab, während zwei entgegengesetzt geladene Teilchen sich anziehen.
Die elektrostatische Kraft wird beschrieben durch das Coulombsche Gesetz
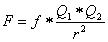
Der Proportionalitätsfaktor ist von Einheitensystem abhängig. In SI - Einheiten
beträgt er im Vakuum
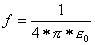
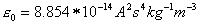
Nach dem Coulombschen Gesetz existiert zwischen Elektron und Proton die elektrische Anziehungskraft
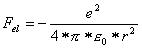
Das Elektron bewegt sich mit einer Bahngeschwindigkeit v und besitzt demnach eine Zentrifugalkraft
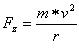
wobei m die Masse des Elektrons ist (m = 0.9109534*10-30 kg).
Für eine stabile Umlaufbahn muss die Zentrifugalkraft entgegengesetzt gleich der elektrischen
Anziehungskraft sein, somit muss folgendes gelten:
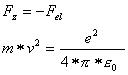
Die Energie des Elektrons auf der Kreisbahn setzt sich zusammen aus kinetischer Energie und potentieller
Energie:
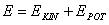
Die kinetische Energie ist definiert als:
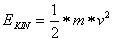
Die potentielle Energie ist die Energie, die durch die elektrische Anziehung zwischen Proton und Elektron
zustande kommt:
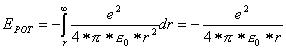
Die Gesamtenergie des Elektrons ist somit gegeben durch:
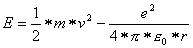
Die Energie ist somit nur vom Radius der Kreisbahn abhängig. Das Elektron kann sich
laut Bohr auf allen Bahnen mit r = 0 bis r =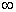 
.
Die klassische Mechanik akzeptierte das Bohrsche Atommodell, die klassische Elektrodynamik jedoch
widersprach ihm. Das Elektron würde Enegie in Form von Licht abstrahlen und dadurch an Geschwindigkeit
verlieren. Dies führt dazu, dass das Elektron in einer Spiralbewegung in den Kern stürzt.
Bohr reagierte nun und stellte folgende Annahme:
Das Elektron darf sich nicht auf beliebigen Bahnen aufhalten. Er kann sich nur auf ganz bestimmten
Bahnen strahlungsfrei bewegen. Diese erlaubten Elektronenbahnen sind solche, deren Bahndrehimpuls mvr
immer ein ganzzahliges Vielfaches einer Grundeinheit des Drehimpulses ist.
Die Grundeinheit des
Bahndrehimpulses ist
Die mathematische Form des Bohrschen Postulats lautet:
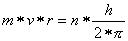
n ist eine natürliche Zahl und wird Quantenzahl genannt.
Umformung obiger Gleichung ergibt
Auflösung nach dem Radius r ergibt
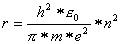
Indem wir die Werte für die Konstanten einsetzen, erhalten wir
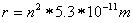
Das Elektron darf sich somit nur in ganz bestimmten Abständen vom Kern entfernt aufhalten, damit
es strahlungsfrei kreisen kann. Setzt man die verschiedenen n - Werte ein, so erhält die erlaubten
Radien 0.053 nm, 0.212 nm, 0.477nm, 0.848 nm usw. .
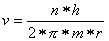
Für die Geschwindigkeit gibt es ebenfalls Einschränkungen. Das Elektron sollte eine
Bahngeschwindigkeit haben, die folgender Gleichung genügt:
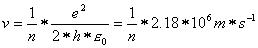
Und schliesslich sollte das Elektron ganz bestimmte Energiewerte besitzen, die durch folgende Gleichung festgelegt sind:
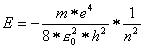
Das Elektron ganz somit nur ganz bestimmte Energiewerte annehmen, die durch die Quantenzahl n
festgelegt sind. Diese Quantelung hat somit zur Folge, dass das Elektron sich nur auf wohldefinierten
Bahnen aufhalten kann.
ChemGlobe
