

|
Ionisierungsenergie |
| ⬇ |
Die Ionisierungsenergie I eines Atoms, ist die Mindestenergie, die notwendig ist, um diesem Atom ein Elektron komplett zu entreissen. Die Dimension von I ist die Energie. Die Einheit für I ist eV.
Im folgenden wird Ionisierungsenergie öfters mit I abgekürzt.
Bei der Ionisierung eines Atoms entsteht ein positiv geladenes Ion.
Atom + I → Atom+ + e-
Die Ionisierungsenergie ist eine Eigenschaft, die sich direkt auf die Elektronen in den Atomen bezieht. Daher ist eine periodische Veränderung von I im Periodensystem zu erwarten. Die Ionisierungsenergie ist, anders gesagt, ein Mass für die Festigkeit, mit der ein Elektron an ein Atom gebunden ist.
Natürlich kann ein einem bereits ionisierten Atom nochmals ein Elektron entreissen. Wenn man einem Ion mit der Ladung 1+ noch ein Elektron entreisst, braucht man soviel Energie wie die '2. Ionisierungsenergie'. Das gleiche gilt für die 3., 4. usw. Ionisierungen.
Bemerkung: dieser Paragraph vernachlässigt die Effekte, die durch Orbitalsymmetrie auftreten. Dies sind Effekte, die zustande kommen, weil Elektronen einer gleichen Schale sich nicht in den gleichen energetischen Zuständen befinden, obwohl sie auf der gleichen Schale sind. Siehe dazu den nächsten Paragraph.
Die Elektronen der letzten Schale werden von der Kernladung an das Atom gebunden. Desto grösser die Kernladung und desto kleiner die Distanz der äusseren Elektronen zum Kern ist, desto grösser ist die Ionisierungsenergie. Stellen wir uns nun vor, wir würden auf der äusseren Elektronenschale herumfliegen. Wenn wir dann die elektrostatische Kraft messen, die auf uns wirkt, dann ist es die Kraft, die von den Protonen im Atomkern ausgeübt wird, minus den Anteil, der von den unter uns liegenden Elektronen 'absorbiert' wird.
Die auf diese Art 'übrigbleibende' Kraft auf der letzten Schale, wird von jedem einzelnen Elektron 'gespürt'. Desto grösser diese Kraft ist oder desto kleiner die Distanz zu den positiven Ladungen ist, desto grösser ist die Energiemenge, die man aufwenden muss, um ein Elektron aus der letzten Schale auszureissen.
Die Tendenz innerhalb einer Periode wirkt sich folgendermassen aus (Beispiel: Periode 2):
| Atom | Li | C | F |
|---|---|---|---|
| Situtation im Grundzustand | 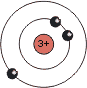 |
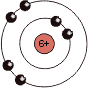 |
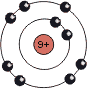 |
| Gruppe (neue IUPAC-Empfehlung) | 1 | 14 | 17 |
| elektrostatische Kraft auf Valenzelektronen |  |
||
| elektrostatische Kraft auf Valenzelektronen | ionisierungsenergie |
+-------+----------+------+ | Table Headings | Here | +-------+----------+------+ | Sub | Headings | Too | +=======+==========+======+ | cell | column spanning | + spans +----------+------+ | rows | normal | cell | +-------+----------+------+ | multi | cells can be | | line | formatted | | | paragraphs | | cells | | | too | | +-------+-----------------+
| Atom | Li | C | F |
|---|---|---|---|
| Situtation im Grundzustand |

 |
 |
 |
| Gruppe (neue IUPAC-Empfehlung) | 1 | 14 | 17 |
| elektrostatische Kraft auf Valenzelektronen | |||
Die Zunahme der elektrostatischen Kraft auf der letzten Schale innerhalb einer Periode bewirkt, dass die Atome in einer Periode, mit steigender Ordnungszahl, eine steigende Ionisierungsenergie haben.
Die Tendenz innerhalb einer Gruppe wirkt sich folgendermassen aus (hier Gruppe 1)
| Atom | Situtation im Grundzustand | Periode | 'übrigbleibende' elektrostatische Kraft |
|---|---|---|---|
| Li |  |
2 | |
| Na |  |
3 | |
| K |  |
4 |
Innerhalb einer Gruppe, bleibt bei steigender Ordnungszahl, die elektrostatische Kraft auf der letzten Schale zwar unverändert, dafür steigt aber die Distanz zum Atomkern, und somit zu den positiven Ladungen. Demnach wird die elektrostatische Kraft auf der letzten Schale desto kleiner, je höher die Ordnungszahl ist. Man redet in einem solchen Fall von effektiver Kraft.
Aus diesen beiden Tatsachen kann man schliessen, dass Helium (rechts oben in der Periodentafel) das Element mit der höchsten Ionisierungsenergie ist, und Francium (links unten in der Periodentafel) das Element mit der tiefsten Ionisierungsenergie ist.
Zur Erinnerung: Diese Herleitung stimmt noch nicht ganz, da dies eine kontinuierliche Veränderung der Ionisierungsenergie für steigende Ordnungszahl innerhalb einer Periode bedeuten würde, was aber nicht der Fall ist. Dazu die Erklärung im nächsten Paragraph.
Für eine korrekte theoretische Herleitung der Ionisierungsenergien, müssen Erklärungen anhand der Orbitaltheorie benutzt werden.
Orbitale, die ganz oder genau halb gefüllt sind, besitzen eine höhere Stabilität. Daher gibt es jeweils einen Sprung von 2s2 auf 2s22p1 und von 2s22p3 auf 2s22p4.
| Element | 2s | 2p | Ionisierungsenergie |
|---|---|---|---|
| Li | |
|
 |
| Be | |
|
|
| B | |
|
|
| C | |
|
|
| N | |
|
|
| O | |
|
|
| F | |
|
|
| Ne | |
|
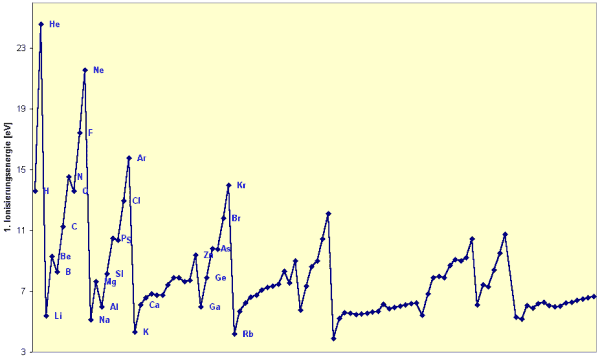
Dateidownload: pse_tab_1ion.csv (1 kB) enthält die 1. Ionisierungsenergie für alle Elemente der 6 ersten Perioden. Layout wie im Bild unten. (Format: Strichkomma getrennte Liste)
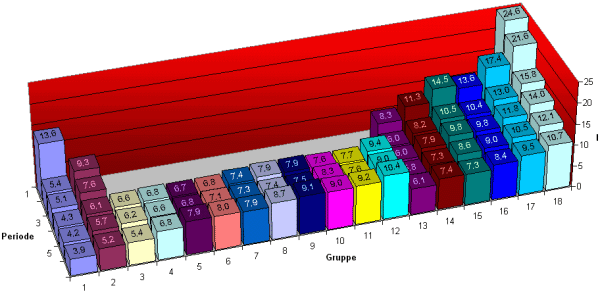
Dateidownload: pse_list_1ion.csv (2 kB) enthält die 1. Ionisierungsenergie für alle die Elemente 1-102. Layout wie im Bild unten. (Format: Strichkomma getrennte Liste)
Innerhalb von ChemGlobe
| ⬆ |
| ⬆ |
| © 1998–2022 ChemGlobe |